Question

Which of the following is a quadratic equation

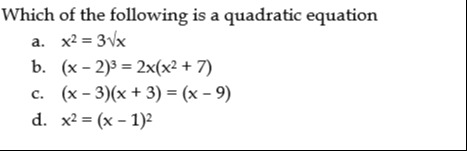
• A. $x^2 = 3\sqrt{x}$
• B. $(x-2)^3 = 2x(x^2 + 7)$
• C. $(x-3)(x+3) = (x-9)$
• D. $x^2 = (x-1)^2$

Answer 1

Answer: (C)

c

Answer 2

A quadratic equation is an equation of the form $ax^2 + bx + c = 0$, where $a \neq 0$.

1. $x^2 = 3\sqrt{x}$ is not a polynomial equation in $x$ due to $\sqrt{x}$.
2. $(x-2)^3 = 2x(x^2 + 7)$ simplifies to $x^3 + 6x^2 + 2x + 8 = 0$, which is a cubic equation (highest power of $x$ is 3).
3. $(x-3)(x+3) = (x-9)$ simplifies to $x^2 - 9 = x - 9$, which further simplifies to $x^2 - x = 0$. This is of the form $ax^2 + bx + c = 0$ with $a=1 \neq 0$, $b=-1$, $c=0$. Hence, it is a quadratic equation.
4. $x^2 = (x-1)^2$ simplifies to $x^2 = x^2 - 2x + 1$, which further simplifies to $2x - 1 = 0$. This is a linear equation (highest power of $x$ is 1).

Therefore, only option c is a quadratic equation.