Question

Which of the following has the greatest number of atoms?

A. ${\text{1}}\,{\text{g}}$ of butane $\left( {{{\text{C}}_{\text{4}}}{{\text{H}}_{{\text{10}}}}} \right)$
B. ${\text{1}}\,{\text{g}}$ of nitrogen $\left( {{{\text{N}}_2}} \right)$
C. ${\text{1}}\,{\text{g}}$ of silver $\left( {{\text{Ag}}} \right)$
D. ${\text{1}}\,{\text{g}}$ of water $\left( {{{\text{H}}_2}{\text{O}}} \right)$

Answer 1

According to the Avogadro, one mole of any substance have $\,6.02 \times {10^{23}}$ atoms, ions, or molecules. This number $\,6.02 \times {10^{23}}$ is known as Avogadro number. The total number of atoms can be determined by multiplying the moles of a substance with Avogadro number.

Step by step answer: The number of moles in a substance is determined by using the mole formula which is as follows:

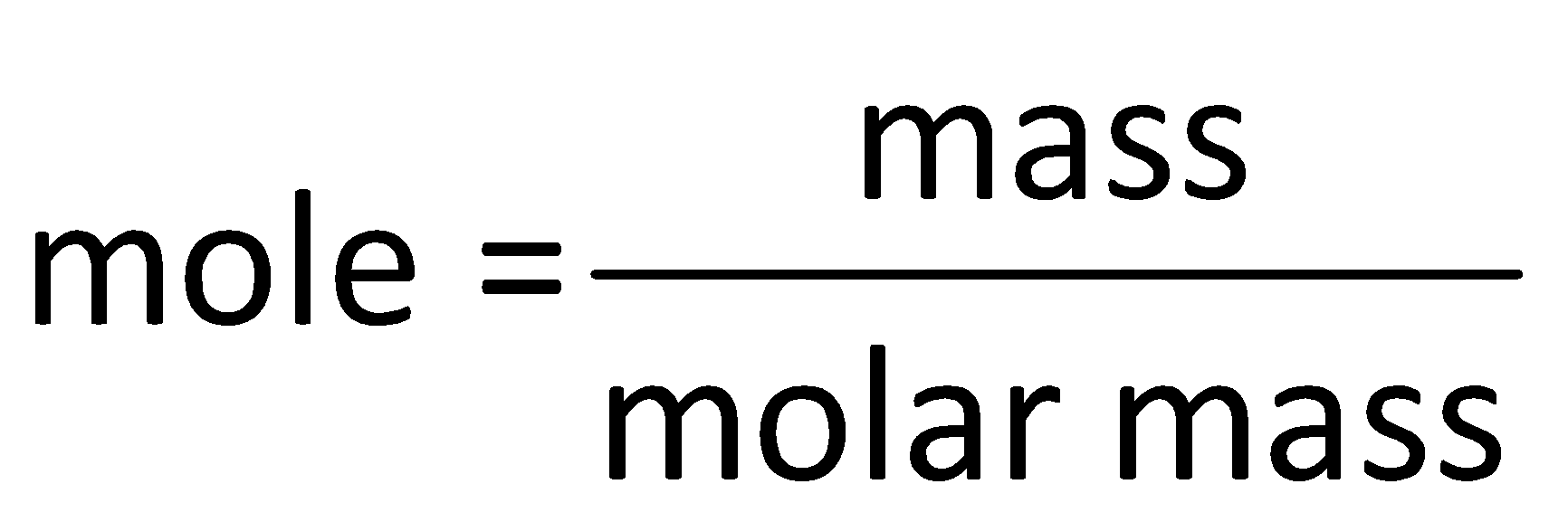
Determine the mole in ${\text{1}}\,{\text{g}}$ of butane as follows:
Substitute ${\text{1}}\,{\text{g}}$ for mass and $58\,{\text{g/mol}}$ for molar mass.
${\text{mole}}\,\,{\text{of }}{{\text{C}}_4}{{\text{H}}_{10}}{\text{ = }}\,\dfrac{{{\text{1 g}}}}{{{\text{58 g/mol}}}}$
${\text{mole}}\,\,{\text{of }}{{\text{C}}_4}{{\text{H}}_{10}}{\text{ = }}\,{\text{0}}{\text{.017}}\,{\text{mol}}$

Multiply the mole of butane with Avogadro number to determine the total number of molecules.

${\text{Molecules}}\,{\text{of }}{{\text{C}}_4}{{\text{H}}_{10}}{\text{ = }}\,{\text{0}}{\text{.017}}\,{\text{mol}} \times {\text{6}}{\text{.02}} \times {\text{1}}{{\text{0}}^{23}}{\text{molecules/mol}}$
${\text{Molecules}}\,\,{\text{of }}{{\text{C}}_4}{{\text{H}}_{10}}{\text{ = }}\,1.04 \times {\text{1}}{{\text{0}}^{22}}$
So, the number of molecules in ${\text{1}}\,{\text{g}}$of butane is $1.04 \times {\text{1}}{{\text{0}}^{22}}$.
One molecule of butane has $14$atoms. So, the total number atoms are as follows:
$1.04 \times {\text{1}}{{\text{0}}^{22}} \times {\text{1}}4$
$14.6 \times {\text{1}}{{\text{0}}^{22}}{\text{atoms}}$
So, the number of atoms in ${\text{1}}\,{\text{g}}$ of butane is$14.6 \times {\text{1}}{{\text{0}}^{22}}$.

Determine the mole in ${\text{1}}\,{\text{g}}$ of nitrogen as follows:

Substitute ${\text{1}}\,{\text{g}}$ for mass and $14\,{\text{g/mol}}$ for molar mass.
${\text{mole}}\,\,{\text{of }}{{\text{N}}_2}{\text{ = }}\,\dfrac{{{\text{1 g}}}}{{{\text{14 g/mol}}}}$
${\text{mole}}\,\,{\text{of }}{{\text{N}}_2}{\text{ = }}\,{\text{0}}{\text{.071}}\,{\text{mol}}$

Multiply the mole of nitrogen with Avogadro number to determine the total number of molecules.

${\text{molecules}}\,\,{\text{of }}{{\text{N}}_2}{\text{ = }}\,{\text{0}}{\text{.071}}\,{\text{mol}} \times {\text{6}}{\text{.02}} \times {\text{1}}{{\text{0}}^{23}}{\text{molecules/mol}}$
${\text{molecules}}\,\,{\text{of }}{{\text{N}}_2}{\text{ = }}\,4.{\text{3}} \times {\text{1}}{{\text{0}}^{22}}$

So, the number of molecules in ${\text{1}}\,{\text{g}}$ of nitrogen is $4.3 \times {\text{1}}{{\text{0}}^{22}}$.

One molecule of nitrogen has $2$atoms.
$= 4.3 \times {\text{1}}{{\text{0}}^{22}} \times 2$
$= 8.6 \times {\text{1}}{{\text{0}}^{22}}$
So, the number of atoms in ${\text{1}}\,{\text{g}}$ of nitrogen is $8.6 \times {\text{1}}{{\text{0}}^{22}}$.
Determine the mole in ${\text{1}}\,{\text{g}}$ of silver as follows:
Substitute ${\text{1}}\,{\text{g}}$ for mass and $108\,{\text{g/mol}}$ for molar mass.
${\text{mole}}\,\,{\text{of Ag}}\,{\text{ = }}\,\,\dfrac{{{\text{1 g}}}}{{108\,{\text{g/mol}}}}$
${\text{mole}}\,\,{\text{of Ag}}\,{\text{ = }}\,\,{\text{9}}{\text{.259}} \times {\text{1}}{{\text{0}}^{ - 3}}\,{\text{mol}}$
Multiply the mole of silver with Avogadro number to determine the total number of molecules.
${\text{molecules}}\,\,{\text{of Ag}}\,{\text{ = }}\,\,{\text{9}}{\text{.259}} \times {\text{1}}{{\text{0}}^{ - 3}}\,{\text{mol}} \times {\text{6}}{\text{.02}} \times {\text{1}}{{\text{0}}^{23}}{\text{molecules/mol}}$
${\text{molecules}}\,{\text{of Ag}}\,{\text{ = }}\,\,0.55 \times {\text{1}}{{\text{0}}^{22}}$
One molecule of silver has one atom.
${\text{Atoms}}\,{\text{of Ag}}\,{\text{ = }}\,\,1\, \times 0.55 \times {\text{1}}{{\text{0}}^{22}}$
${\text{Atoms}}\,{\text{of Ag}}\,{\text{ = }}\,0.55 \times {\text{1}}{{\text{0}}^{22}}$
So, the number of atoms in ${\text{1}}\,{\text{g}}$ of silver is $0.55 \times {\text{1}}{{\text{0}}^{22}}$.
Determine the mole in ${\text{1}}\,{\text{g}}$ of water as follows:
Substitute ${\text{1}}\,{\text{g}}$ for mass and $18\,{\text{g/mol}}$ for molar mass.
${\text{mole}}\,\,{\text{of }}{{\text{H}}_2}{\text{O}}\,{\text{ = }}\,\,\dfrac{{{\text{1 g}}}}{{18\,{\text{g/mol}}}}$
${\text{mole}}\,\,{\text{of }}{{\text{H}}_2}{\text{O}}\,{\text{ = }}\,\,0.055\,{\text{mol}}$
Multiply the mole of water with Avogadro number to determine the total number of molecules.
${\text{molecules}}\,\,{\text{of }}{{\text{H}}_2}{\text{O}}\,{\text{ = }}\,\,0.055\,{\text{mol}} \times {\text{6}}{\text{.02}} \times {\text{1}}{{\text{0}}^{23}}{\text{molecules/mol}}$
${\text{molecules}}\,\,{\text{of }}{{\text{H}}_2}{\text{O}}\,\,{\text{ = }}\,\,3.3 \times {\text{1}}{{\text{0}}^{22}}$
So, the number of molecules in ${\text{1}}\,{\text{g}}$ of water is $3.3 \times {\text{1}}{{\text{0}}^{22}}$.
One molecule of water has $3$atoms.
No. of atoms $= 3 \times 3.3 \times {\text{1}}{{\text{0}}^{22}}$
No. of atoms $= 9.9 \times {\text{1}}{{\text{0}}^{22}}{\text{atoms}}$
So, the number of atoms in ${\text{1}}\,{\text{g}}$ of water is$9.9 \times {\text{1}}{{\text{0}}^{22}}$.
${\text{1}}\,{\text{g}}$ of butane has the highest number of moles so, option (B), (C), (D) are incorrect.
Therefore, option (A) ${\text{1}}\,{\text{g}}$ of butane$\left( {{{\text{C}}_{\text{4}}}{{\text{H}}_{{\text{10}}}}} \right)$, is correct.

Note: Atomicity also denotes the number of atoms in a substance. Here, the gram amount of each substance is given so, the total number of atoms is determined by multiplying the moles with Avogadro's number and number of atoms in one molecule. If the gram amount is not given the total number of atoms can be determined by adding the number of atoms of a substance.