Question
Question: Which of the following has regular tetrahedral shape? a.) \(I_{3}^{-}\) b.) \(S{{F}_{4}}\) c....
Which of the following has regular tetrahedral shape?
a.) I3−
b.) SF4
c.) [BF4]−
d.) XeF4
Solution
Hint: We can get the shape of any compound with the help of hybridization. The shape of the compound depends primarily on the no. of bond pairs and lone pairs, but every unique pair of bonds and lone there is specific value hybridization.
Complete step by step solution:
H=2(V+M−C+A)
H= hybridization
V= valance on the central atom
M= monovalent group
C = charge on cation
A= charge on anion
We can predict the shape of any molecule or compound by its hybridization. After hybridization by this table we can find the shape of the compound.
The table is given below: -
| H= l.p.+ b.p. | Hybridization state | Shapes |
|---|---|---|
| 2 | sp | Linear |
| 3 | sp2 | Trigonal planar |
| 4 | sp3 | Tetrahedral or pyramidal or v- shaped |
| 5 | sp3d | Trigonal bipyramidal or T- shaped or linear |
| 6 | sp3d2 | Octahedral or square pyramid or planner |
| 7 | sp3d3 | Pentagonal bipyramidal or distorted or distorted pentagonal bipyramid |
Here l.p refers to Lone pair electrons and b.p refers to bond pair electrons.
Now we can solve the shapes of compounds by this above table.
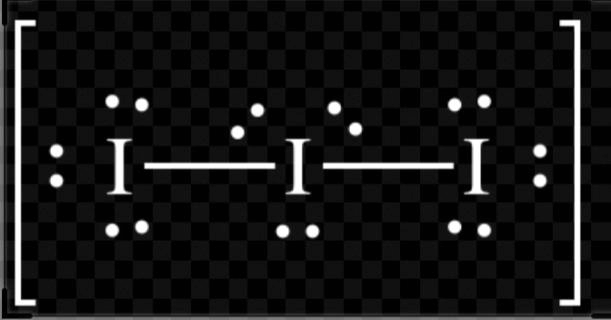
A. I3−
H=2(V+M−C+A)
H=2(7+2−0+1)
H=210= 5
So, hybridization of I3−= sp3d
Shape= linear
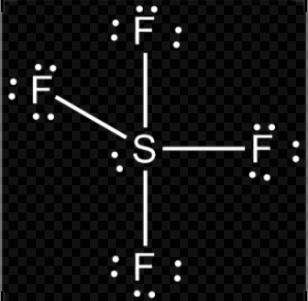
B. SF4
H=2(V+M−C+A)
H=2(6+4−0+0)
H=210
So, hybridization of SF4 = sp3d
Shape = trigonal bipyramidal
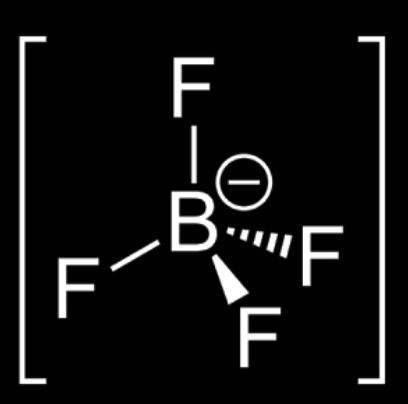
C. [BF4]−
H=2(V+M−C+A)
H=2(3+4−2+1) H=2(5+4−0+1)H=210
H=26= 3
So, the Hybridization of molecule [BF4]−= sp2
Shape = tetrahedral
D. XeF4
H=2(V+M−C+A)
H=2(5+4−0+1)
H=210= 5
So, the hybridization of molecule XeF4= sp3d
And shape = trigonal bipyramidal
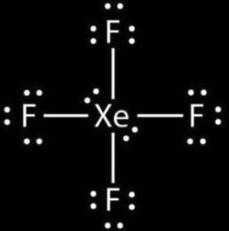
Therefore, boron tetrafluoride has the regular shape of tetrahedral.
Note:
-Check the valence electron properly while calculation of hybridisation
-Check the charge of cation and anions on the molecule. It should also be taken into account
-Check the hybridization properly for concluding the final geometry of the molecule.
