Question
Question: Which of the following graphs between potential energy between two nucleons \(U(x)\) and distance be...
Which of the following graphs between potential energy between two nucleons U(x) and distance between the atoms (x) is correct?
A.

B.
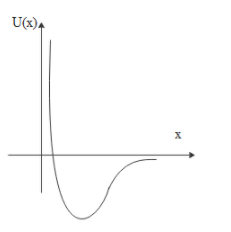
C.
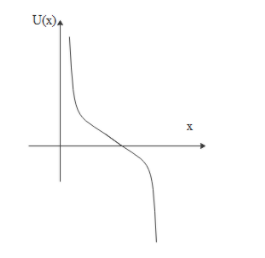
D.
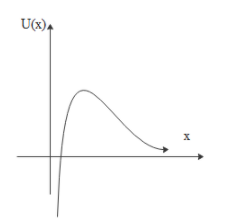
Solution
In nucleus, protons and neutrons are bound together by nuclear force, which is strong enough to overcome the repulsion between protons. The nuclear force is attractive for distances larger than 0.8fm and repulsive if they are separated by distance lesser than this.
Formula Used:
U(x)=x12a+x6b
Complete step-by-step answer :
The average net potential energy of all the protons and neutrons in the nucleus due to nuclear forces between them is known as nuclear potential energy.
The relation between nuclear potential energy and separation between nucleons is given by
U(x)=x12a+x6b
Wherea and b are constants
U(x)=Potential energy
x=Separation between nucleons
We differentiate this equation and equate to zero to obtain points of maxima and minima
dxdU(x)=−12x13a+(x7−6b)=0
⇒x6=b2a
We can note here that for
x→0 ; U→+∞
And for
x→∞; U→0 from negative side
These conditions are best represented by graph B
Therefore, option B is correct.
Additional information: Nucleons are either neutron or proton.
The nuclear force is a force acting between the protons and neutrons of atoms. The nuclear force is the force that binds the protons and neutrons in a nucleus. This force can be either between protons and protons, neutrons and protons or neutrons and neutrons. This force is what holds the nucleus together.
Note : The range of a nuclear force is very short. At 0.8 Fermi, the distance between particles in a nucleus is very small. At this separation, the nuclear force is much stronger than the repulsive Coulomb’s force that pushes the particles away. However, if the distance is more than 2.5 Fermi, nuclear force is practically non-existent.
