Question
Question: Which of the following graphs are of functions? A. 
B.
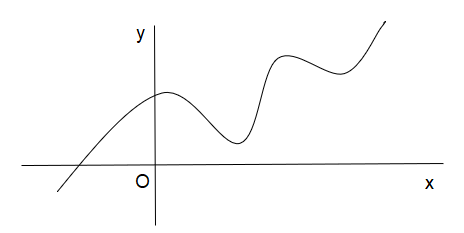
C.
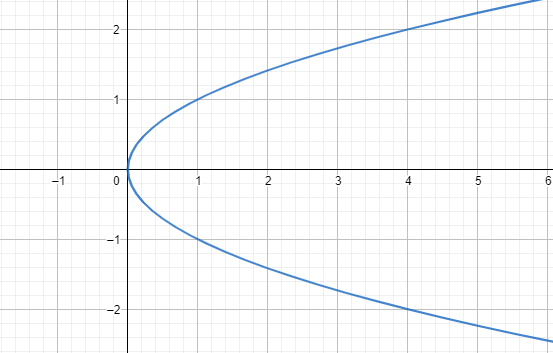
D.
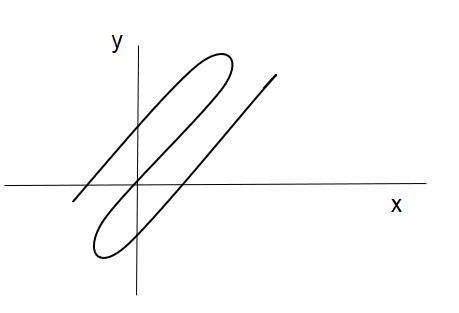
Solution
We have to find if the function is one-one or not. We use vertical line tests to determine whether the line intersects the function at more than one point or not. Depending on the number of intersecting points we determine if the curve is a function or not.
Complete step by step solution:
We need to find if the curves are a one-one function or not.
This means for a particular value of x, we will get only one value of y.
So, every value of x can be projected to a particular value of y.
In case of one-one function, we can have an inverse always irrespective of the function.
In case many-one functions, we can’t have an inverse function.
Let’s assume that g(a)=g(b)=c for an arbitrary function g(x) .
This is a two-one function. The domain has two values a,b that give the same value of c in range. Condition is a=b.
When we are taking the inverse, we get one value in the domain which gives two values in range. That can't function as g−1(c)=a and g−1(c)=b but a=b.
The vertical line test gives that for the function f(x) if any vertical line parallel to the Y-axis represented as x=k an infinite extension cuts the graph more than once then the graph is not a function.
For the given images the third and fourth graph can’t be a function as a vertical line cuts them at more than one point.
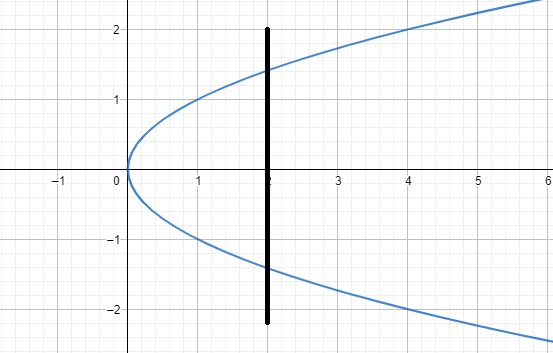
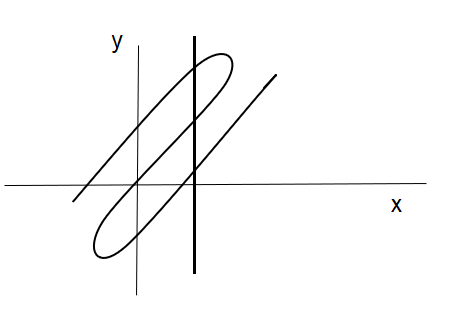
In the first picture the line cuts the curve in two points and in the next image it cuts at three points. That’s why these aren’t functions.
Rest two curves are functions as the line cuts them at only one point.
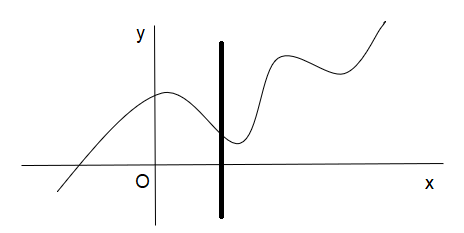
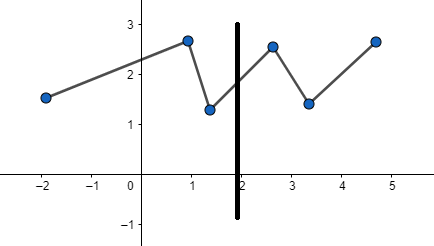
Note: If the vertical line intersects the graph of a function in all places at exactly one point, then the given function should have an inverse that is also a function. We say this function passes the vertical line test.
