Question

Which of the following graph truly represents the titration of KCl solution against $AgNO_3$ solution?

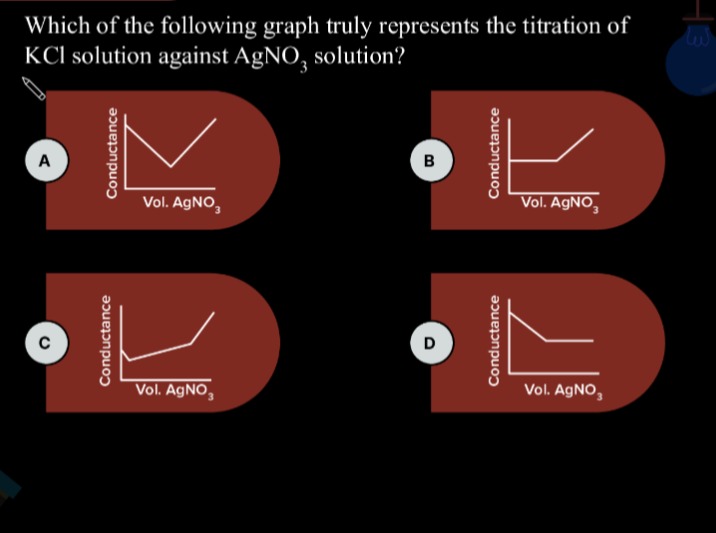
• A. Graph A shows a decrease followed by an increase, forming a V-shape with the increasing segment having a steeper slope than the decreasing segment. This matches our analysis.
• B. Graph B shows a constant conductance followed by an increase. This is incorrect.
• C. Graph C shows a decrease followed by an increase, but the initial decrease is not linear, and the increase is also not linear in the initial part. The shape is generally correct, but the linearity of the segments is expected in ideal conductometric titrations.
• D. Graph D shows a decrease followed by a constant conductance. This is incorrect.

Answer 1

Answer: (A)

Graph A

Answer 2

The titration of KCl solution against $AgNO_3$ solution is a conductometric titration. The reaction is:

$KCl(aq) + AgNO_3(aq) \rightarrow AgCl(s) + KNO_3(aq)$

Initially, the solution contains $K^+$ and $Cl^-$ ions. The conductance of the solution is due to these ions. As $AgNO_3$ is added, $Ag^+$ ions react with $Cl^-$ ions to form insoluble AgCl precipitate. The ions in the solution are $K^+$, $Cl^-$, and $NO_3^-$ (from added $AgNO_3$). Effectively, $Cl^-$ ions are removed from the solution and replaced by $NO_3^-$ ions. The molar conductivity of $Cl^-$ ions ($\lambda_{Cl^-} \approx 76.3 \text{ S cm}^2 \text{ mol}^{-1}$) is slightly higher than that of $NO_3^-$ ions ($\lambda_{NO_3^-} \approx 71.4 \text{ S cm}^2 \text{ mol}^{-1}$). Therefore, as $Cl^-$ ions are replaced by $NO_3^-$ ions, the conductance of the solution decreases. This decrease continues until all $Cl^-$ ions have been precipitated, which is the equivalence point.

At the equivalence point, all $Cl^-$ ions have reacted with $Ag^+$ ions. The solution contains $K^+$ and $NO_3^-$ ions. The conductance is at a minimum at the equivalence point because the highly mobile $Cl^-$ ions have been removed and replaced by less mobile $NO_3^-$ ions, and no excess ions from the titrant have been added yet.

After the equivalence point, excess $AgNO_3$ is added to the solution. The solution now contains $K^+$, $NO_3^-$, and excess $Ag^+$ and $NO_3^-$ ions. The addition of $Ag^+$ and $NO_3^-$ ions increases the total number of ions in the solution, and these ions are mobile. The molar conductivity of $Ag^+$ ions is approximately $61.9 \text{ S cm}^2 \text{ mol}^{-1}$, and that of $NO_3^-$ ions is approximately $71.4 \text{ S cm}^2 \text{ mol}^{-1}$. The addition of these ions leads to an increase in the conductance of the solution.

Therefore, the graph of conductance versus the volume of $AgNO_3$ added should show an initial decrease in conductance before the equivalence point, reaching a minimum at the equivalence point, and then an increase in conductance after the equivalence point. This results in a V-shaped graph.

Comparing the slopes of the two segments:

Before the equivalence point, the decrease in conductance is due to the replacement of $Cl^-$ by $NO_3^-$. The change in molar conductivity is approximately $\lambda_{NO_3^-} - \lambda_{Cl^-} \approx 71.4 - 76.3 = -4.9$.

After the equivalence point, the increase in conductance is due to the addition of $Ag^+$ and $NO_3^-$. The increase in molar conductivity per mole of $AgNO_3$ added is approximately $\lambda_{Ag^+} + \lambda_{NO_3^-} \approx 61.9 + 71.4 = 133.3$.

Considering the concentration of the titrant and the volume change, the slopes are proportional to these values. If the titrant concentration is the same, and neglecting volume change for qualitative comparison of slopes, the magnitude of the slope after the equivalence point is significantly larger than the magnitude of the slope before the equivalence point.

Based on the expected linear segments in conductometric titrations and the relative slopes, graph A is the most accurate representation of the titration. The initial decrease is due to the replacement of $Cl^-$ by $NO_3^-$, and the subsequent increase is due to the addition of excess $Ag^+$ and $NO_3^-$. The steeper slope after the equivalence point is consistent with the higher combined molar conductivity of $Ag^+$ and $NO_3^-$ compared to the difference in molar conductivity between $Cl^-$ and $NO_3^-$.