Question

Which of the following expressions is known as Clausius inequality?
A. $\oint {\dfrac{{dq}}{T}} \le 0$
B. $\oint {\dfrac{{dq}}{T} = 0}$
C. $\oint {\dfrac{T}{{dq}}} \le 0$
D. $\oint {\dfrac{{dq}}{T}} \ge \le 0$

Answer 1

Clausius equality and inequality are two terms which come into picture while finding the closed integral of the ratio of change of heat to the temperature of a thermodynamic system.

Complete step by step answer:
Assume:
$d{Q_1}$ is the amount of heat supplied to both the heat engines.
$d{Q_2}$ and $d{Q_2}^\prime$ be the amount of heat rejected to the sink by reversible and irreversible heat engines respectively.
${T_1}$ and ${T_2}$ are the temperatures of the heat source and sink respectively.
$d{W_R}$ and $d{W_I}$ are the work produced by reversible and irreversible heat engines respectively.
${\rm{H}}{{\rm{E}}_R}$ and ${\rm{H}}{{\rm{E}}_I}$ represents reversible and irreversible heat engine respectively.
Consider two heat engines, one is reversible heat engine and other is irreversible heat engine and both of them are operating between same temperature levels ${T_1}$ and ${T_2}$.

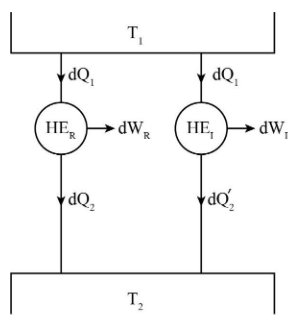
Carnot theorem states that if many heat engines are working under constant temperature source and constant temperature sink then the efficiency of reversible heat engines will always be high if compared to irreversible heat engines.
${\eta _R} > {\eta _I}$……(1)
The efficiencies of reversible and irreversible heat engines as shown in figure are given as
${\eta _R} = \dfrac{{d{W_R}}}{{d{Q_1}}}$
$\Rightarrow{\eta _I} = \dfrac{{d{W_I}}}{{d{Q_1}}}$
Substitute $\dfrac{{d{W_R}}}{{d{Q_1}}}$ for ${\eta _R}$ and $\dfrac{{d{W_I}}}{{d{Q_1}}}$ for ${\eta _I}$ in equation (1).
$\dfrac{{d{W_R}}}{{d{Q_1}}} > \dfrac{{d{W_I}}}{{d{Q_1}}}$……(2)
Using first law of thermodynamics for ${\rm{H}}{{\rm{E}}_R}$ and ${\rm{H}}{{\rm{E}}_I}$ respectively.

$$d{W_R} = d{Q_1} - d{Q_2}\\\ \Rightarrow d{W_I} = d{Q_1} - d{Q_2}^\prime$$

Substitute $d{Q_1} - d{Q_2}$ for $d{W_R}$ and $d{Q_1} - d{Q_2}^\prime$ for $d{W_I}$ in equation (2).

\dfrac{{d{Q_1} - d{Q_2}_{}}}{{d{Q_1}}} > \dfrac{{d{Q_1} - d{Q_2}^\prime }}{{d{Q_1}}}\\\ \Rightarrow - \dfrac{{d{Q_2}}}{{d{Q_1}}} > - \dfrac{{d{Q_2}^\prime }}{{d{Q_1}}}\\\ \Rightarrow\dfrac{{d{Q_2}}}{{d{Q_1}}} < \dfrac{{d{Q_2}^\prime }}{{d{Q_1}}}\\\ \Rightarrow d{Q_2} < d{Q_2}^\prime $$……(3) Expanding the relation $$\oint {\dfrac{{dQ}}{T}} $$ for irreversible heat engines. $$\oint {\dfrac{{dQ}}{T}} = \dfrac{{d{Q_2}}}{{{T_1}}} - \dfrac{{d{Q_2}^\prime }}{{{T_2}}}$$ From equation (3), it is clear that the heat rejected by reversible heat engines is less than the heat rejected by the irreversible heat engine. Hence the term $$\left( {\dfrac{{d{Q_2}}}{{{T_1}}} - \dfrac{{d{Q_2}^\prime }}{{{T_2}}}} \right)$$ becomes less than zero. $\oint {\dfrac{{dQ}}{T}} = \dfrac{{d{Q_2}}}{{{T_1}}} - \dfrac{{d{Q_2}^\prime }}{{{T_2}}}\\\ \Rightarrow\oint {\dfrac{{dQ}}{T}} < 0 $ Writing the above equation in per unit mass form. $\oint {\dfrac{{dq}}{T}} < 0$ **Therefore the expression for Clausius inequality is given by $\oint {\dfrac{{dq}}{T}} < 0$ and the option (A) is correct.** **Note:** : We have to note that the term $\oint {\dfrac{{dq}}{T}} $ is less than or equal to zero to make the system feasible in nature but if it became more than zero then it can be said that system is impossible in nature.