Question

Which of the following examples exhibits zero displacement with non-zero distance?
A) A runner running one round on a circular track
B) A cyclist riding on a straight road
C) An aeroplane cursing in air
D) None of these

Answer 1

Distance travelled is the measurement of the actual path transverse for reaching from one point to another, whereas displacement is the minimum distance between these two points. If in this question we get to point out the case in which the displacement is zero, that is the starting and end points are the same, then the question is solved.

Formula used:
Circumference of the circle $= 2\pi r$
where $r$ is the radius of the circle.

Complete step by step answer:
If a runner runs a single round around a circular track the total distance becomes $= 2\pi r$ where $r$ is the radius of the circle. But the displacement of the runner becomes zero as after completing one round in the track the start and the end points become the same, and distance between them is zero.

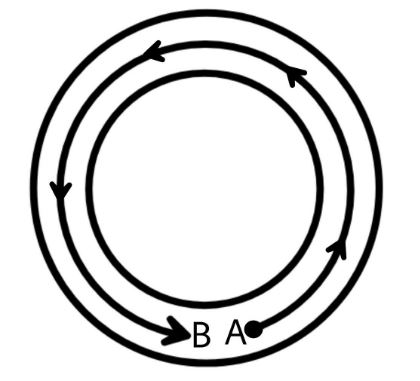
In the above figure the point A and b are the same just for simplicity I have made them different thus the starting point and the end point of the runner becomes equal.For the cyclist riding in the straight road the distance and the displacement become equal for the rider as the road is a straight path.

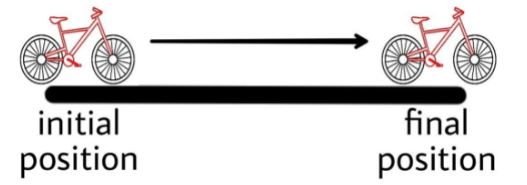
Here in the above diagram the initial and the final position are just separated by a straight path because of the straight road.For a plane cursing through air the distance and displacement remain the same as the plane travels in a straight-line path at some angle to the ground.

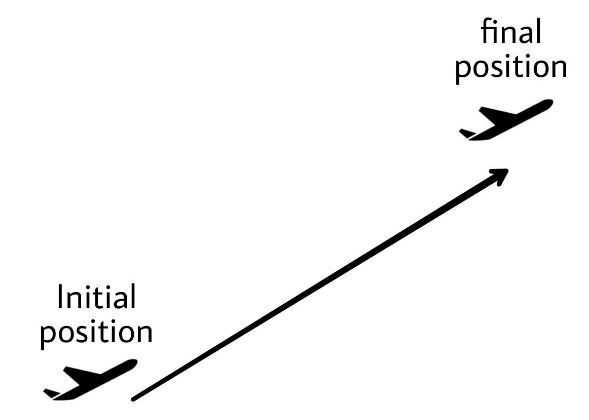
From the above diagram it is clear that the distance and displacement remain the same and we can find the value by using simple trigonometry.
Therefore, the correct option is A.

Note: A major time in circular motion the displacement is zero, but sometimes the object which is moving in a circular path may not stop at the starting point but somewhere else from the starting point. In such cases we will encounter a net displacement for sure as the initial and final points of the object are not the same, and the displacement can be found just by simply calculating the distance between the initial and final point.