Question

Which of the following energy level diagram for ${\left[ {{\text{Fe(F}}{{\text{)}}_{\text{6}}}} \right]^{3 - }}$ is correct on basis of the crystal field theory?
A.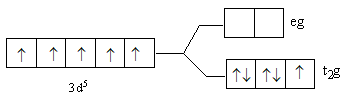
B.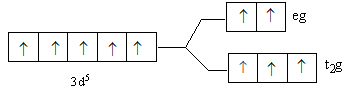
C.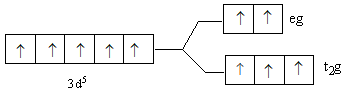
D.

Answer 1

The d-orbitals of the metal remain degenerate in absence of ligand filed. Crystal field theory describes the removal of the degeneracy of orbitals of metal in presence of a ligand field. After the splitting electrons of metal get rearranged in these orbitals. So, first, we will determine the number of electrons in d-orbitals of metal after the formation of the complex. Then we will arrange these electrons in these orbitals.

Complete step-by-step answer: Iron is a transition element and atomic number of iron $26$. Its valence electronic configuration is, ${\text{3}}{{\text{d}}^6}{\text{4}}{{\text{s}}^{\text{2}}}$ .

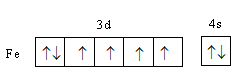
We will determine the charge on the metal as follows:

Suppose the charge of the metal is x. Charge of fluorine ligand is $- 1$so,
$x\, + \,\left( {6 \times - 1} \right) = + 3$
$x = - 3 + 6$
$x = + 3$
So, the charge on the metal is $+ 3$.
So, Fe is present as ${\text{F}}{{\text{e}}^{{\text{3 + }}}}$in ${\left[ {{\text{Fe(F}}{{\text{)}}_{\text{6}}}} \right]^{3 - }}$ .
The valance electronic configuration of ${\text{F}}{{\text{e}}^{{\text{3 + }}}}$ is ${\text{3}}{{\text{d}}^5}$,

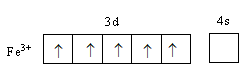
When six fluorine ligands approach the iron metal an octahedral complex forms. Iron metal’s d-orbitals split into two sets of two and three orbitals. In octahedral geometry of the complex, ligand approach from the axis and the orbitals ${{\text{d}}_{{{\text{x}}^{\text{2}}} - {{\text{y}}^{\text{2}}}}}$ and ${{\text{d}}_{{{\text{z}}^{\text{2}}}}}$ are present on the axis whereas${{\text{d}}_{{\text{xy}}}}$,${{\text{d}}_{{\text{zy}}}}$ and ${{\text{d}}_{{\text{xz}}}}$ orbitals lie in between the axes. So, the energy of two orbitals ${{\text{d}}_{{{\text{x}}^{\text{2}}} - {{\text{y}}^{\text{2}}}}}$ and ${{\text{d}}_{{{\text{z}}^{\text{2}}}}}$ increases due to the ligands and the energy of three orbitals decreases. As a result, five degenerated-orbitals lose that degeneracy and split into two groups.
The splitting of d-orbitals of iron and then filling of electrons is shown as follows:

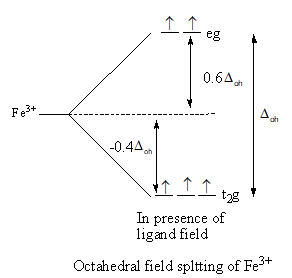
So, after the formation of the complex ${\left[ {{\text{Fe(F}}{{\text{)}}_{\text{6}}}} \right]^{3 - }}$ according to the crystal field theory, three electrons are present in ${{\text{t}}_{\text{2}}}{\text{g}}$ level and two electrons are present in ${\text{eg}}$.

So, the energy level diagram C for is correct on basis of the crystal field theory for ${\left[ {{\text{Fe(F}}{{\text{)}}_{\text{6}}}} \right]^{3 - }}$.

Note: The lower level having three d-orbitals is known as ${{\text{t}}_{\text{2}}}{\text{g}}$ and upper level having two d-orbitals is known as ${\text{eg}}$. Fluorine is a weak ligand, so it is not able to cause paring of metal d-electrons. Thus, we fill the three electrons in lower than two electrons in upper energy level. In case of a strong ligand, lower energy levels get filled first. If after filling the lower level, the electrons remain then the upper level is filled. The ligands are arranged according to their field strength, this series is known as spectrochemical series.