Question

Which of the following corresponds to the principal value branch of ${{\tan }^{-1}} {x}$?
A. $\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)$
B. $\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right]$
C. \left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right) - \left\\{ 0 \right\\}
D. $\left( 0,\pi \right)$

Answer 1

We explain the function ${{\tan }^{-1}}$. We express the inverse function of tan in the form of $arc\tan \left( x \right)={{\tan }^{-1}}x$. We draw the graph of ${{\tan }^{-1}}\left( x \right)$ and take an example of ${{\tan }^{-1}}1$ to understand the exact and general solution.

Complete step by step answer:
The given expression is the inverse function of trigonometric ratio tan. The arcus function represents the angle which on ratio tan gives the value.So, $arc\tan \left( x \right)={{\tan }^{-1}}x$. If $arc\tan \left( x \right)=\alpha$ then we can say $\tan \alpha =x$.Each of the trigonometric functions is periodic in the real part of its argument, running through all its values twice in each interval of $2\pi$. The general solution for that value where $\tan \alpha =x$ will be $n\pi +\alpha ,n\in \mathbb{Z}$.

But for $arc\tan \left( x \right)$, we won’t find the general solution. We use the principal value. For ratio tan we have $-\dfrac{\pi }{2} < arc\tan \left( x \right) < \dfrac{\pi }{2}$.The graph of the function is,

$arc\tan \left( x \right)=\alpha$ gives the angle $\alpha$ behind the ratio. We now take the example of $x=1$ in the function of $arc\tan \left( x \right)$. Let the angle be $\theta$ for which $arc\tan \left( 1 \right)=\theta$. This gives $\tan \theta =1$. Putting the value in the graph of $arc\tan \left( x \right)$, we get $\theta =45$.

For this we take the line of $x=1$ and see the intersection of the line with the graph $arc\tan \left( x \right)$.

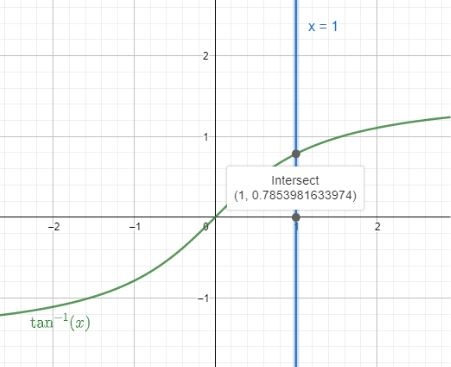
The correct option is A.

Note: Although for elementary knowledge the principal domain is enough to solve the problem. But if mentioned to find the general solution then the domain changes to $-\dfrac{\pi }{2} < arc\tan \left( x \right) < \dfrac{\pi }{2}$. In that case we have to use the formula $x=n\pi +a$ for $\tan \left( x \right)=\tan a$ where $-\dfrac{\pi }{2} < a < \dfrac{\pi }{2}$.