Question
Question: Which of the following correctly describes the variation of the speed \(v\) and acceleration \(a\) o...
Which of the following correctly describes the variation of the speed v and acceleration a of a point mass falling vertically in a viscous medium that applies a force F=−kv, where k is a constant, on the body? (The graphs are schematic and are not drawn to scale)
A. 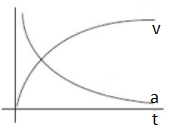
B. 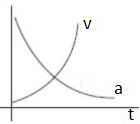
C. 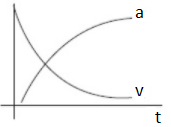
D. 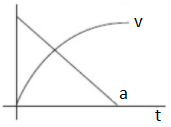
Solution
When a body(point mass) is free-falling from a defined distance from the surface of the earth the acceleration of the body is the same as the acceleration due to gravity acting on the point mass. The velocity of the body acts in the opposite direction of the motion of the body. By balancing the forces the equations for the values of acceleration and velocity can be easily obtained.
Complete step by step answer:
When we refer to the free body diagram of a free-falling body as shown in the diagram
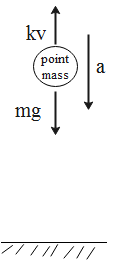
We get a balanced equation for forces as,
ma=mg−kv.....(1)
So when there is maximum acceleration (a), the velocity (v) of the body will be the least (zero).
So, the maximum velocity vmax of point mass will be,
mg−kvmax=0⇒vmax=kmg.....(2)
By reconsidering equation (1);
Diving both the sides by mass (m)
a=g−mkv
we can simplify the equation as,
dtdv=g−αv
Where, α is an assumed constant equivalent to mk
dt=g−αvdv
Integrating both the side in a definite range,
∫0tdt=∫0vg−αvdv⇒t=−α1ln[g−αv]0v⇒−αt=ln(gg−αv)⇒e−αt=gg−αv
By putting the value of α
