Question

Which is the smallest wavelength that will be observed in the spectra of ${ H }_{ e }^{ + }$ ion?

Answer 1

The smallest wavelength in the spectra of atoms corresponds to the Lyman series of the spectral series. The atomic number of ${ H }_{ e }^{ + }$ion is 2.

Formula used:
$\dfrac{1}{\lambda }=R{{Z}^{2}}\left( \dfrac{1}{n_{1}^{2}}-\dfrac{1}{n_{2}^{2}} \right)$
where
$R$ is the Rydberg constant
$Z$ is the atomic number
${ n }_{ 1 }$ is the orbit to which the electron jumps. ${{n}_{1}}=1,2,3,...\infty$
${ n }_{ 2 }$ is the orbit from which the electron jumps. ${{n}_{2}}={{n}_{1}}+1,{{n}_{1}}+2,{{n}_{1}}+3,...\infty$
$\lambda$ is the wavelength of the corresponding spectral line

Complete step-by-step answer:
When electric current is passed through an atomic gas, the gas emits radiations of certain specific wavelengths. A spectrum is formed and this is called the Line emission spectrum. In this spectrum, groups of spectral lines are observed. These groups are named as spectral series. According to increasing wavelength, these series are named as Lyman series, Blamer series, Paschen series, Brackett series and Pfund series.
When electric current is passed through ${ H }_{ e }^{ + }$ ion, we observe all the spectral series mentioned above. Each spectral line in a spectral series corresponds to a certain wavelength. To obtain the smallest wavelength in the series, we have to concentrate on the Lyman series because this series comes first in the increasing order of wavelengths in the spectrum. We also have to go for the excitation from infinity to the first orbit to obtain the smallest wavelength out of the different excitations happening in the Lyman series. The following diagram explains the same.

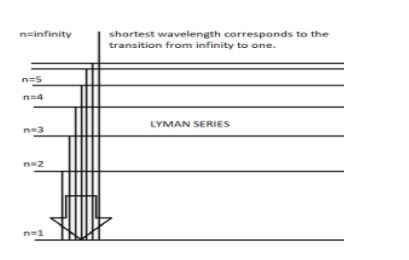
Rydberg equation is given by:
$\dfrac{1}{\lambda }=R{{Z}^{2}}\left( \dfrac{1}{n_{1}^{2}}-\dfrac{1}{n_{2}^{2}} \right)$
Here,
$R=1.0987\times {{10}^{7}}{{m}^{-1}}$
$Z=2$ (atomic number of ${ H }_{ e }^{ + }$ion is 2)
${{n}_{1}}=1$ (for Lyman series)
${{n}_{2}}=\infty$ (for smallest wavelength)
Substituting the values given above, we have:

& \dfrac{1}{\lambda }=1.0987\times {{10}^{7}}\times {{2}^{2}}\times \left( \dfrac{1}{{{1}^{2}}}-\dfrac{1}{{{\infty }^{2}}} \right) \\\ & \dfrac{1}{\lambda }=1.0987\times {{10}^{7}}\times 4\times (1-0) \\\ & \dfrac{1}{\lambda }=1.0987\times {{10}^{7}}\times 4 \\\ & \lambda =\dfrac{1}{1.0987\times 4\times {{10}^{7}}}=0.2275\times {{10}^{-7}}=22.75\times {{10}^{-9}}m\quad \\\ \end{aligned}$$ The answer close to the calculated value is $22.2nm$. **Note:** Students should not get confused with the atomic number of ${ H }_{ e }^{ + }$ ion. It is the same as the atomic number of Helium. Atomic number is dependent only on the number of protons and not the number of lost/gained electrons. Students should also note that for calculating the smallest wavelength, they should substitute values in Lyman series and not any others series because Lyman series lies in the ultraviolet region.