Question

Which crystal lattice has the most efficient packing efficiency?

Answer 1

Hint: Hcp and ccp structure have 4 spheres in the unit cell, bcc structure has 2 and simple cubic structure has 1.
Packing efficiency is increased when a greater number of spheres are there in a unit cell.
Packing efficiency of simple cubic structure = $\dfrac{Volume\,occupied\,by\,spheres\,in\,unit\,cell}{Volume\,of\,unit\,cell}\times 100$
Complete answer:
- Packing efficiency is the percentage of total space filled by the particles.
To calculate the packing efficiency of hcp/ccp structure, let the unit cell edge length be ‘a’ and face diagonal AC=b

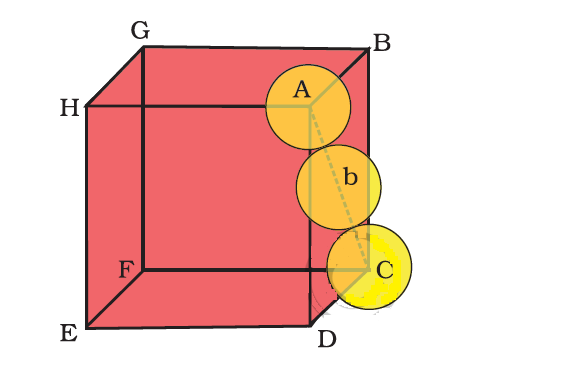
Now, using Pythagoras theorem , in $\Delta ABC$
$A{{C}^{2}}=B{{C}^{2}}+A{{B}^{2}}$
${{b}^{2}}={{a}^{2}}+{{a}^{2}}$
Therefore, ${{b}^{2}}=2{{a}^{2}}$
or by taking the square roots, we have $b=\sqrt{2}a$ ……………………….(1)
Now, if ‘r’ is the radius of the sphere, then from the diagram we can say that ,
b = 4r ……..(2)
From equation numbers (1) and (2), we have
$\sqrt{2}a=4r$
or $a=\dfrac{4r}{\sqrt{2}}=2\sqrt{2}r$ ……….(3)
We know that in each unit cell of ccp structure there are 4 spheres.
Hence, total volume occupied by 4 spheres will be $=4\times \dfrac{4}{3}\pi {{r}^{3}}$
This will be equal to $\dfrac{16}{3}\pi {{r}^{3}}$ ……………….(4)
Now, volume of unit cell = ${{a}^{3}}={{\left( 2\sqrt{2}r \right)}^{3}}$ ……..[Since, from equation (3)]
Thus, solving this we get, volume of unit cell = $16\sqrt{2}{{r}^{3}}$ ……(5)
Therefore, packing efficiency of ccp/hcp structure = $\dfrac{Volume\,occupied\,by\,4\,spheres\,in\,unit\,cell}{Volume\,of\,unit\,cell}\times 100$
By substituting the values from equation (4) and (5),
Packing efficiency of ccp/hcp structure = $\dfrac{\left( \dfrac{16}{3}\pi {{r}^{3}} \right)}{16\sqrt{2}{{r}^{3}}}\times 100=\dfrac{\left( \dfrac{16}{3}\pi \right)}{16\sqrt{2}}\times 100=74$%
Now, to calculate the packing efficiency of bcc (body centered cubic) structure, let body diagonal AF = c. From figure, it is clear that the atom at the centre will be in touch with the other two atoms diagonally arranged.

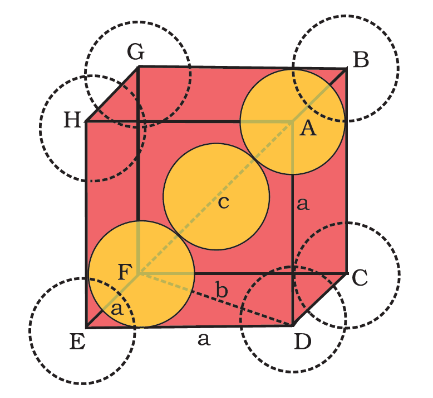
Now, using Pythagoras theorem , in $\Delta EFD$
$D{{F}^{2}}=D{{E}^{2}}+E{{F}^{2}}$
${{b}^{2}}={{a}^{2}}+{{a}^{2}}$
Therefore, ${{b}^{2}}=2{{a}^{2}}$
or by taking the square roots, we have $b=\sqrt{2}a$ ……………………….(1)
Now, using Pythagoras theorem , in $\Delta ABC$
$A{{C}^{2}}=B{{C}^{2}}+A{{B}^{2}}$
${{b}^{2}}={{a}^{2}}+{{a}^{2}}$
Therefore, ${{b}^{2}}=2{{a}^{2}}$
or by taking the square roots, we have $c=\sqrt{3}a$ ……………………….(2)
Now, if ‘r’ is the radius of the sphere, then from the diagram we can say that ,
c = 4r ……..(3)
From equation numbers (2) and (3), we have
$\sqrt{3}a=4r$
or $a=\dfrac{4r}{\sqrt{3}}$ ……….(4)
We know that in each unit cell of bcc structure there are 2 spheres.
Hence, total volume occupied by 4 spheres will be $=2\times \dfrac{4}{3}\pi {{r}^{3}}$
This will be equal to $\dfrac{8}{3}\pi {{r}^{3}}$ ……………….(5)
Now, volume of unit cell = ${{a}^{3}}={{\left( \dfrac{4r}{\sqrt{3}} \right)}^{3}}$ ……..[Since, from equation (4)]
Thus, solving this we get, volume of unit cell = $\dfrac{64}{3\sqrt{3}}{{r}^{3}}$ ……(6)
Therefore, packing efficiency of bcc structure = $\dfrac{Volume\,occupied\,by\,2\,spheres\,in\,unit\,cell}{Volume\,of\,unit\,cell}\times 100$
By substituting the values from equation (5) and (6),
Packing efficiency of bcc structure = $\dfrac{\left( \dfrac{8}{3}\pi {{r}^{3}} \right)}{{{\left( {64}/{3\sqrt{3}}\; \right)}^{3}}}\times 100=\dfrac{\left( \dfrac{8}{3}\pi \right)}{{64}/{3\sqrt{3}}\;}\times 100=68$%.
Let us now calculate the packing efficiency of a simple cubic structure.
From the figure, it is clear that atoms are located at the corners of the unit cell.

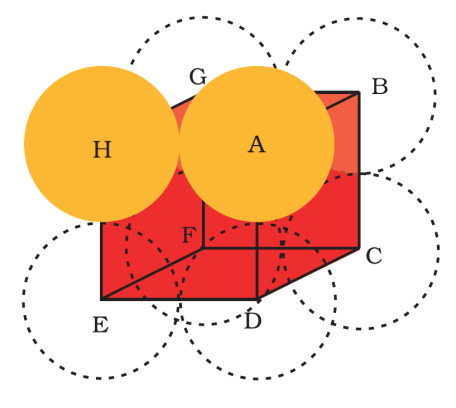
If ‘r’ is the radius of sphere, then from the diagram that two spheres touch each other on edge of the unit cell, a = 2r ……………(1)
We know that in each unit cell of bcc structure, there is one sphere.
Thus, total volume occupied by sphere will be $=\dfrac{4}{3}\pi {{r}^{3}}$ ……….(2)
Now, volume of unit cell = ${{a}^{3}}={{\left( 2r \right)}^{3}}$ ……..[Since, from equation (1)]
Thus, solving this we get, volume of unit cell = $8{{r}^{3}}$ ……(3)
Therefore, packing efficiency of simple cubic structure = $\dfrac{Volume\,occupied\,by\,sphere\,in\,unit\,cell}{Volume\,of\,unit\,cell}\times 100$
By substituting the values from equation (2) and (3),
Packing efficiency of bcc structure = $\dfrac{\left( \dfrac{4}{3}\pi {{r}^{3}} \right)}{8{{r}^{3}}}\times 100=\dfrac{\left( \dfrac{4}{3}\pi \right)}{8}\times 100=52.4$%.
Hence, we can conclude that packing efficiency of hcp/ccp is maximum that is 74%.

Note:
Packing efficiency of hcp/ccp structure is 74%.
Packing efficiency of bcc structure is 68% and of simple cubic structure is 52.4%.
Constituent particles are arranged in different patterns in a unit cell. There will always be some vacant space called void. Packing efficiency depends on the number of atoms present.