Question

Where will the ball come in the equilibrium?

A) At a depth ${\text{ }}\dfrac{{{h_0}}}{2}{\text{ }}$from top
B) At the bottom of the vessel
C) At a depth${\text{ }}\dfrac{{3{h_0}}}{4}{\text{ }}$from top
D) The ball will never be at equilibrium

Answer 1

The force exerted by a fluid on a body that is fully or partially submerged in it is called the buoyant force. This is the force responsible for the floating of a body. The equilibrium position is when all the forces acting on the body cancel each other. To find the answer to this question we have to find the position where the forces acting on the ball become equal and opposite.

Formula used:
${F_B} = PA$
Where ${\text{ }}{F_B}{\text{ }}$is the buoyant force acting on the body immersed in water, ${\text{ P }}$stands for the pressure, ${\text{ A }}$stands for the area of the liquid surface.
$P = h\rho g$
Where ${\text{ P }}$stands for the pressure,${\text{ h }}$stands for the height of the liquid,${\text{ }}\rho {\text{ }}$stands for the density of the liquid, and ${\text{ }}g{\text{ }}$is the acceleration due to gravity.

Complete step by step solution:
When the ball is in a liquid, the force acting on that ball will be the buoyant force exerted by the liquid. The buoyant force is the result of the pressure exerted by the fluid. At equilibrium, the net force acting on the ball will be zero. To find the equilibrium we have to find the height at which the forces cancel each other.
Let us assume that ${\text{ }}{F_1}{\text{ }}$and${\text{ }}{F_2}{\text{ }}$ are the forces acting on the ball from opposite directions as shown in the figure.

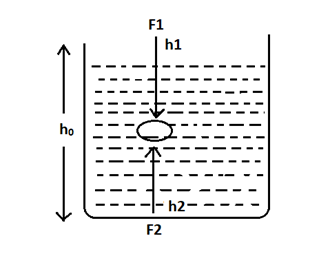
Equilibrium is the position where${\text{ }}{{\text{F}}_1} = {{\text{F}}_2}$
The buoyant force${\text{ F }}$is given by,
$F = PA$
We know that,${\text{ P = h}}\rho {\text{g}}$
$\therefore {F_1} = {h_1}\rho gA$
And, ${\text{ }}{{\text{F}}_2} = {h_2}\rho gA$
At equilibrium ${\text{ }}{{\text{F}}_1} = {{\text{F}}_2}$
$\Rightarrow {h_1}\rho gA = {h_2}\rho gA$
From this we get that, at equilibrium
${h_1} = {h_2}$
From the figure, we know that
${h_1} + {h_2} = {h_0}$
This means that the equilibrium position is the midpoint of ${\text{ }}{h_0}$
That is at, ${\text{ }}\dfrac{{{h_0}}}{2}$

The answer is Option (A): At a depth ${\text{ }}\dfrac{{{h_0}}}{2}{\text{ }}$ from top.

Note: According to Archimedes principle, the buoyant force acting on a body will be equal to the weight of the liquid displaced by that body. The buoyant force depends on the volume of the body immersed and the density of the fluid. Submarines, ships, hot air balloons etc. make use of buoyant force. Fishes float in water with the help of buoyant force. Buoyancy is a very important factor for swimmers also.