Question

Where will be the centre of mass on combining two masses 4Kg and 8Kg?
A. Towards 4kg
B. Towards 8kg
C. Between 4kg and 8kg
D. Data Insufficient

Answer 1

Hint: Imagine that you have 4kg on your one hand and 8kg on another hand. You will experience that you are bending towards 8kg to balance it. This is due to a shift in centre of mass towards heavy objects.

Complete step by step answer:
To proceed further to our question first we discuss the meaning of centre of mass.
Centre of mass: The point of a rigid body of a system where its total mass can be concentrated is known as centre of mass of that rigid body of a system.
The centre of mass of a rigid body can be given by x, y and z coordinates.
Position vector of centre of mass is given by:
${{r}_{cm}}=\dfrac{{{m}_{1}}{{r}_{1}}+{{m}_{2}}{{r}_{2}}+.....+{{m}_{n}}{{r}_{n}}}{{{m}_{1}}+{{m}_{2}}+.....+{{m}_{n}}}$
${{r}_{cm}}=$position vector of centre of mass
Centre of mass of two particles:
If ${{m}_{1}}$ and ${{m}_{2}}$are two particles lying on a plane. Then their centre of mass always exists on the line joining them.
${{x}_{cm}}=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}}{{{m}_{1}}+{{m}_{2}}}$
And
${{y}_{cm}}=\dfrac{{{m}_{1}}{{y}_{1}}+{{m}_{2}}{{y}_{2}}}{{{m}_{1}}+{{m}_{2}}}$
Therefore centre of mass must be on $({{x}_{cm}},{{y}_{cm}})$
It is clear from the above formula if there are two equal masses lying on the plane. Then the centre of mass must lie at the midpoint of the line joining them.
It is also clear from above formula that:
$r\propto \dfrac{1}{m}$

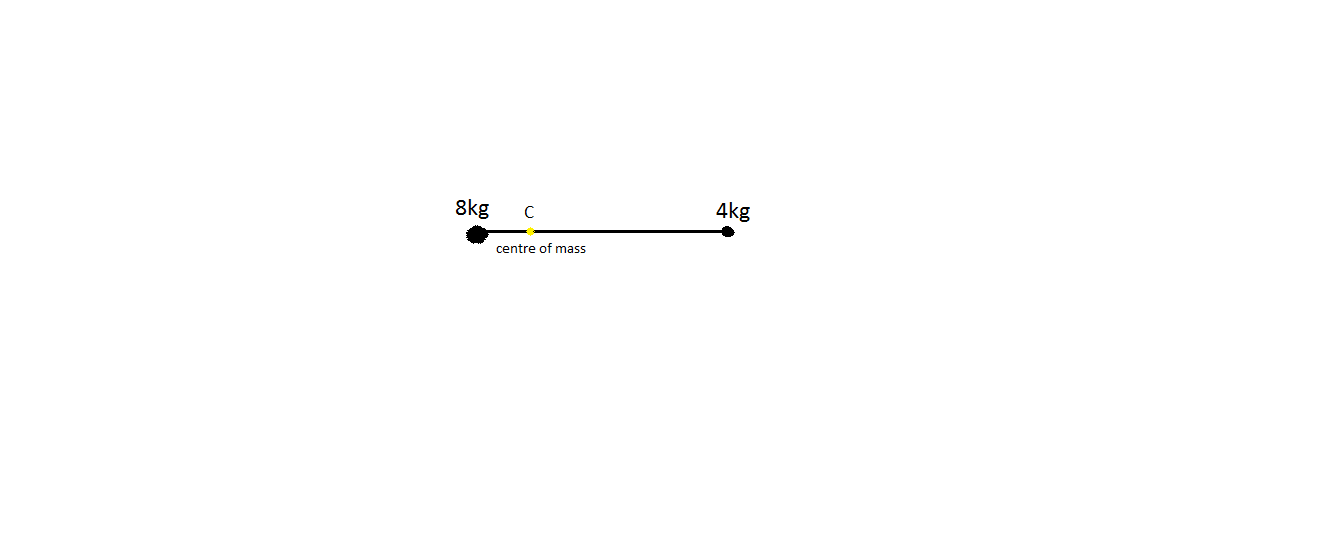
That is if we increase the mass, the centre of mass starts to adjust from its initial position to the heavy object.
Thus in our question there are two objects of mass 4kg and 8kg. Therefore the centre of mass move towards the heavy object i.e. it moves towards the 8kg object.
Hence the correct answer is option B.

Note: When more than one body present in the system centre of mass will shift from lighter body to heavier body.
Centre of mass for a symmetric body always lies at the centre of that body.