Question

Where should a convex lens of focal length 9 cm be placed $\left( {in{\text{ }}cm} \right)$ between two point sources $S_1$ ​and $S_2$ ​ which are $24\;cm$ apart, so that images of both the sources are formed at the same place. You have to find the distance of the lens from $S_1$ or $S_2$ whichever is lesser.

Answer 1

Hint:
- You should know the difference between the images formed in convex to the concave.
- You should know the convex lens equation.

Complete step by step solution:

According to the convex lens equation,
$\dfrac{1}{f}{\text{ }} = {\text{ }}\dfrac{1}{v}{\text{ }} + {\text{ }}\dfrac{1}{u}$ Where, u is the distance from the object, v is the distance from the image and f is the focal length.
It relates the focal length of a lens with the distance of an object placed in front of it and the image formed of that object. All image or object left to the optical point is negative and all image or object on the right side of the optic centre is positive.

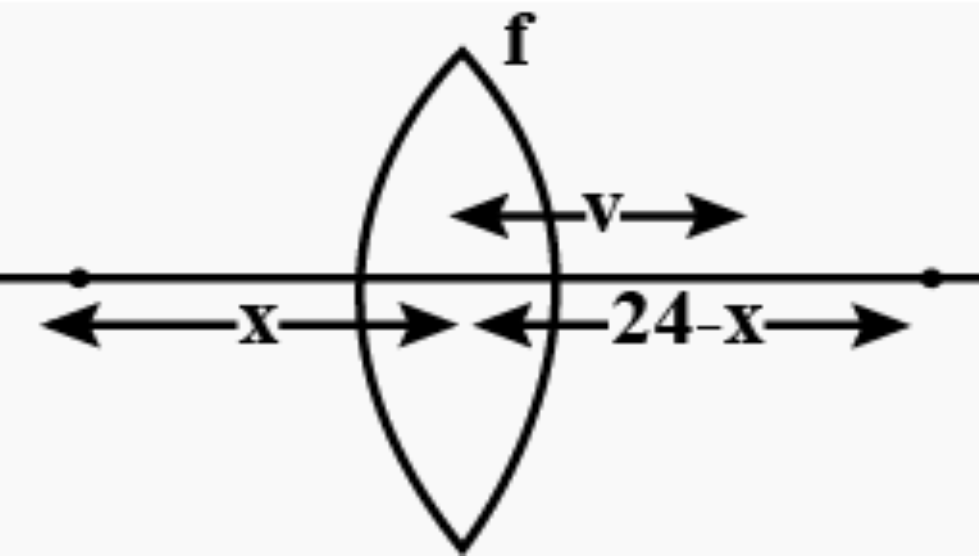
For refraction from left hand source ${S_1}$,
$\dfrac{1}{{ - v}} - \dfrac{1}{{ - x}} = \dfrac{1}{9}$
For refraction from right hand source ${S_2}$,
$\dfrac{1}{{ - v}} - \dfrac{1}{{ - \left( {24 - x} \right)}} = \dfrac{1}{9}$
Adding the equations gives,

${x^2} - 24x + 108 = 0$
Therefore
$x = 6cm$
$x = 18cm$

Smaller distance is 6cm.

Note:
- Memorize basic equations.
- Should have a good conceptual clarity in the image formed in the lens.
- You should be aware of numerical errors.
- You should be aware of negative signs which are used in the solution.