Question
Question: Where is the electric field zero between two opposite charges?...
Where is the electric field zero between two opposite charges?
Solution
A physics field that surrounds electrically charged particles and exerts a force on all other charged particles in the field, either attracting or repelling them, is referred to as an electric field. It can also refer to a system of charged particles' physics field.
Complete step-by-step solution:
At a given distance from a point charge, the electric field is a vector that points away from a positive charge and toward a negative charge. Its magnitude is proportional to the charge and inversely proportional to the distance, according to the inverse square law.
The only place where the field vectors may point in absolutely opposite directions is the line running between the two-point charges. Hence the zero-field position must be there.
The field vectors from both charges point toward the negative charge, thus it can't be between the two opposite charges. It must be on one side of both of them, with the vectors pointing in opposing directions.
For the field from the smaller charge to be equal in magnitude to the field from the larger charge, it must be on the side closer to the smaller charge.
Let's get to algebra now that we've covered geometry. By the square root of its charge to the larger charge, the distance from the smaller charge must be less than the distance from the larger charge. If you know the charge ratio, you can figure out the distance ratio. After you've set up your coordinate system, you'll need to solve a linear problem rather than a quadratic equation.
Additional Information:
Recognize that the 0 potential reference point is infinitely far away from both charges. As a result, when you go to a place equidistant from both charges, you do positive work against one charge's field while doing negative work against the other (since they have an opposite charge). As a result, the total amount of work completed is zero.
Note:
Example:
Two opposite point charges, each of magnitude q are separated by a distance2d. What is the electric potential at a point P mid-way between them?
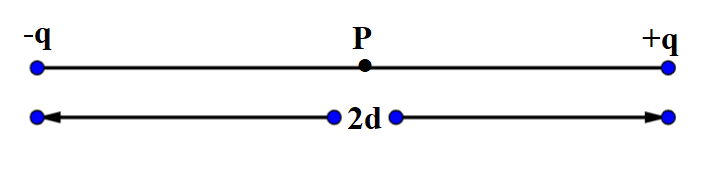
Result:
V+=4πε01dq and V−=−4πε0d1dq
⇒V=V++V−=4πε01dq−4πε01dq=0
So, the potential at P due to opposite charges is 0.
