Question

Where is the centre of Mass of uniform hollow cone?

Answer 1

Use the basic $x=\dfrac{\int z . \sigma d A}{\int \sigma d A}$ to determine a system's centre of mass. The difference between the centre of gravity and the centre of mass will also be known to us. Then, the problem can be solved after performing basic integral calculations.
Formula used:
$x=\dfrac{\int z . \sigma d A}{\int \sigma d A}$

Complete answer:

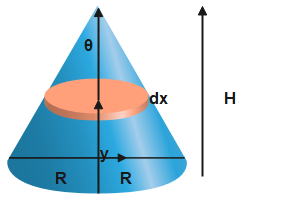
Let the distance from the vertex of the cone to any point on the cone's axis be '$x^{\prime}$.' Let the radius of the base of the cone also be 'R'. And 'h' is already given to be the cone's height. Let's take that 'r' as the distance from the cone axis of any point on the cone, measuring the distance perpendicular to this axis. From the picture, we can find that, using the concept of geometry,
From the picture, using the concept of geometry we can find that,
$\dfrac{r}{R}=\dfrac{z}{h}=\dfrac{l}{L}$ - (1)
Here "I" is the distance of any point on the cone directly from the vertex. Looking at the image here gives you better
understanding.
Let $\sigma$ be the surface density of mass of the cone. Now imagine a circular plane perpendicular to the axis. Its
circumference will be $2 \pi r$. Now an infinitesimal area around the circle is $d A=2 \pi r . d l$ (look at the image).
The center of mass of a system is given by the formula,
$x=\dfrac{\int z . \sigma d A}{\int \sigma d A}$
Substituting the above values in the formula for center of mass, and using relations in equation (i), we obtain,
$x=\dfrac{\int 2 \sigma \cdot \pi r . z . d l}{\int 2 \sigma \cdot \pi r \cdot d l}$
$\Rightarrow x=\dfrac{2 \pi \int_{0}^{h} \sigma \dfrac{R L}{h^{2}} z^{2} d z}{2 \pi \int_{0}^{h} \sigma \dfrac{R L}{h^{2}} z d z}$
Cancelling the like terms, we get
$\Rightarrow x=\dfrac{\int_{0}^{h} z^{2} d z}{\int_{0}^{h} z d z}$
On integrating numerator and denominator separately, we get $\Rightarrow x=\dfrac{\left[\dfrac{z^{3}}{3}\right]_{0}^{h}}{\left[\dfrac{z^{2}}{2}\right]_{0}^{h}}$
On applying the limits and simplifying, we get $\Rightarrow x=\dfrac{\left[\dfrac{h^{3}}{3}-0\right]}{\left[\dfrac{h^{2}}{2}-0\right]}$
$\Rightarrow x=\dfrac{h^{3}}{3} \times \dfrac{2}{h^{2}}$
After solving this, we obtain that, $x=\dfrac{2}{3} \cdot h$
So, this is the final answer.

Note:
Usually, where the masses are discreet, the definition of centre of mass contains summation. But we have to use integration in the event of continuous mass distribution. Convert all the variables into a single variable during integration And set the limits, then.