Question

When $x\le 2,f\left( x \right)=2x+3$ here $f\left( x \right)$ is a polynomial function, therefore it is continuous on R, in particular it is continuous when $x\le 2$ .
When $x>2,f\left( x \right)=2x-3$ here $f\left( x \right)$ is a polynomial function, therefore it is continuous on R, in particular it is continuous when $x>2$ at $x=2$ .

Answer 1

For, $x\le 2,f\left( x \right)=2x+3$ and for $x>2,f\left( x \right)=2x-3$ . Here, our function is f\left( x \right)=\left\\{ \begin{aligned} & 2x+3,x\le 2 \\\ & 2x-3,x>2 \\\ \end{aligned} \right\\} . Calculate the limit value just before and just after $x=2$ . If the limit value exists, then the function is said to be continuous.

Complete step by step answer:
According to the question, we are given two cases for the polynomial $f\left( x \right)$ .
In the ${{1}^{st}}$ case, we have
When $x\le 2,f\left( x \right)=2x+3$ here $f\left( x \right)$ is a polynomial function, therefore it is continuous on R, in particular it is continuous when $x\le 2$ .
Here, we have $f\left( x \right)=2x+3$ for all real values of x less than or equal to 2.
Let us plot the function $f\left( x \right)=2x+3$ on the coordinate axes for all real value of x less than or equal to 2.
$f\left( x \right)=2x+3,x\le 2$ ……………………………………(1)
We can observe that the function $f\left( x \right)$ is a straight line with slope equal to 2 and y intercept equal to 3.

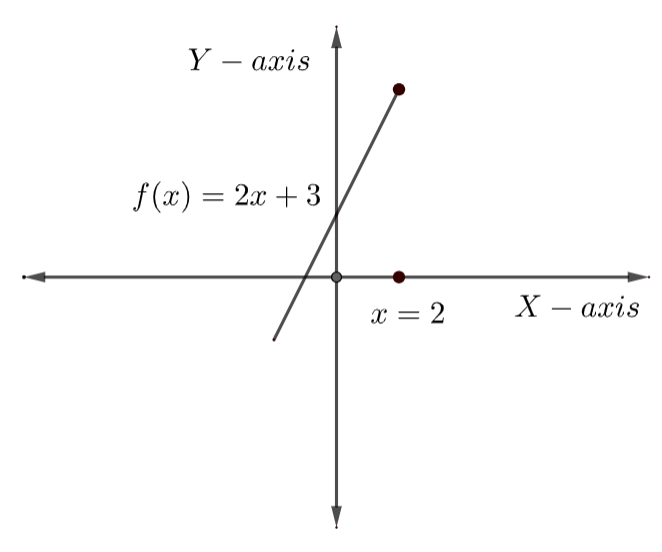
In the ${{2}^{nd}}$ case, we have
When $x>2,f\left( x \right)=2x-3$ here $f\left( x \right)$ is a polynomial function, therefore it is continuous on R, in particular it is continuous when $x>2$ at $x=2$ .
Here, we have $f\left( x \right)=2x-3$ for all real values of x greater than 2.
Let us plot the function $f\left( x \right)=2x+3$ on the coordinate axes for all real value of x greater than 2.
$f\left( x \right)=2x-3,x>2$ ……………………………………(2)
We can observe that the function $f\left( x \right)$ is a straight line with slope equal to 2 and y intercept equal to -3.

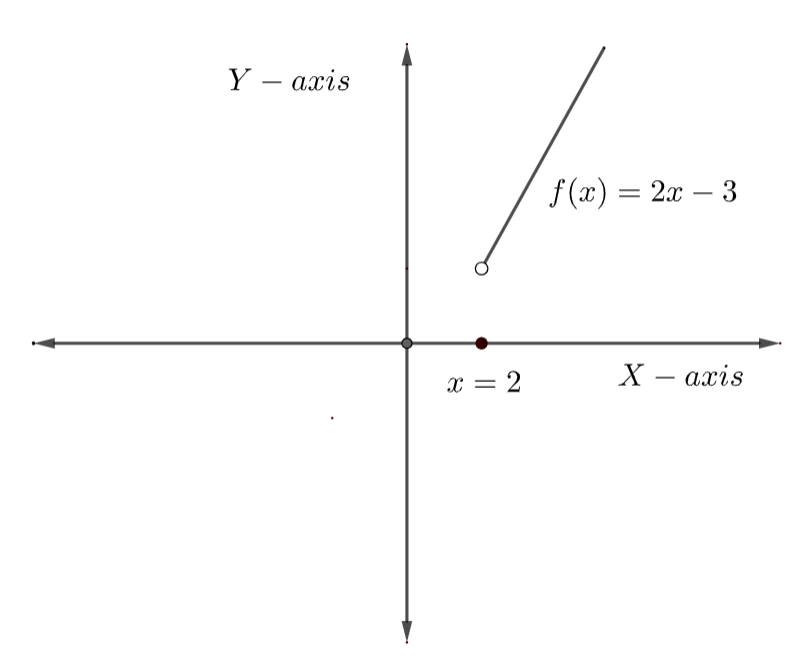
In the above diagram we can observe that there is open dot at $x=2$ . It means the function $f\left( x \right)$ doesn’t take the value $f\left( x \right)=2x-3$ at $x=2$ .
On combining equation (1) and equation (2), we get

& 2x+3,x\le 2 \\\ & 2x-3,x>2 \\\ \end{aligned} \right\\}$$  For the function, to be continuous, the limit must exist at $$x=2$$ . For $$x=2+h$$ where $$h\to 0$$ , we have $$\displaystyle \lim_{h\to 0}2\left( 2+h \right)-3=4-3=1$$ …………………………………………..(3) Similarly, for $$x=2-h$$ where $$h\to 0$$ , we have $$\displaystyle \lim_{h\to 0}2\left( 2-h \right)+3=4+3=7$$ ……………………………………………..(4) Now, from equation (3) and equation (4), we have the limit value just before and just after $$x=2$$ . Therefore, the given function is continuous. **Note:** In this type of question, where we are asked to check the continuity of the function at a specific point. The best way to approach this type of question is to find the value of the limit just before and just after that point. If the value of the limit exists then, the function is said to be continuous.