Solveeit Logo
Login

Question

Question: When two thin lenses of focal lengths \(f_1\) and \(f_2\) are kept coaxially and in contact, prove t...

When two thin lenses of focal lengths f1f_1 and f2f_2 are kept coaxially and in contact, prove that their combined focal length “f” is given by : 1f=1f1+1f2\dfrac{1}{f} = \dfrac{1}{f_1} + \dfrac{1}{f_2}

Explanation

Solution

Choose a point object on the principal axis and use the lens formula to get the location of the image formed by the first lens and then use the image formed by the first lens as the object of the second lens and find the location of the final image. Now using the original object location and the final image location find the focal length of a single lens.

Complete step by step answer:

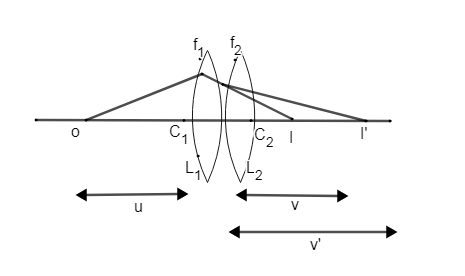
Let us imagine a point object on the principal axis of the two thin lenses as shown in the figure
Let us consider the first lens which has a focal length of f1f_1
We know the lens formula is given by 1v−1u=1f\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}
Where V is the image distance and u is the object distance and f is the focal length of the lens
We get the image distance as: 1v,−1u=1f1\dfrac{1}{v^,} - \dfrac{1}{u} = \dfrac{1}{f_1} where v,v^, is Image distance formed by the first lens.
Now this image formed by the lens act as a virtual object for the second lens which forms the final image of the object at a distance v
Now for the second lens applying lens formula we get:
1v−1v,=1f2\dfrac{1}{v} - \dfrac{1}{v^,} = \dfrac{1}{f_2}
Now we have got the two equations, one for each lens no we know the object distance and the final image distance and the focal length of the lens which forms the image at distance v for the object placed at a distance u can be obtained using lens formula as below:
1v−1u=1f\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}
Now combining the equations of the two lenses we get LHS and RHS as below:
1v−1u=1f1+1f2\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f_1} + \dfrac{1}{f_2}
Now comparing the LHS and RHS we get the by equating the RHS we get as below:
1f1+1f2=1f\dfrac{1}{f_1} + \dfrac{1}{f_2} = \dfrac{1}{f}
Hence we found the value of the focal length of an equivalent single lens which can replace the two lenses given as 1f1+1f2=1f\dfrac{1}{f_1} + \dfrac{1}{f_2} = \dfrac{1}{f}

Note:
One of the possible mistakes that one can make in this kind of problem is that which tends to take the combined focal lens as f1+f2f_1 + f_2 and replace it in the lens formula which is wrong. We don't know the value of the combined focal length when two lengths are placed coaxially. Hence we take one lens at a time and find the object and image distance and then use the image formed as a virtual object for the second lens and find the final image distance, which is the correct method, one should take care of this to get the derivation correct.