Question

When two spheres of equal masses undergo glancing elastic collision with one of them at rest, after collision they will move:
A) Opposite to one another
B) In the same direction
C) together
D) at right angle to each other

Answer 1

We know that, when a body is moving, it will always have momentum which is multiplication of velocity and mass. Now, we can see in the question, one body is moving and the other body is at rest. So, it means there will be momentum of the first body and zero momentum of the second body because as discussed above, it is at rest. Now, by using momentum conservation and energy conservation we can get our answer.

Complete step by solution:
From the above question, we can say,
Initial velocity of the first body is $u$
Now, $\theta$ is the angle of sphere 1 and $\phi$ is the angle of sphere 2 after collision.

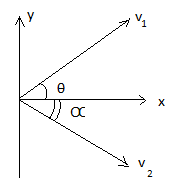
Now, momentum of sphere before collision is $mu$
Now, as the masses of both the spheres are same then,
The total momentum after the collision will be $m{v_1} \cos \theta + m {v_1} \cos \phi$
Now, by momentum conservation,
In $x$ direction,
$m u = m {v_1} \cos \theta + m {v_2} \cos \phi \\\ u = {v_1} \cos \theta + {v_2} \cos \phi ...........\left( 1 \right) \\\$
In $y$ direction,
The initial momentum in this direction will be 0 and final momentum will be $m {v_1} \sin \theta - m {v_2} \sin \phi$
Now, equating them,
$m {v_1} \sin \theta - m {v_2} \sin \phi = 0 \\\ {v_1} \sin \theta - {v_2} \sin \phi = 0.........\left( 2 \right) \\\$
Now, kinetic energy of the system before and after collision will be
${k_i} = \dfrac{1}{2}m {u^2}$ and ${k_f} = \dfrac{1}{2}m v_1^2 + \dfrac{1}{2}m v_2^2$
Now, by equation them,
$\dfrac{1}{2}m {u^2} = \dfrac{1}{2}m v_1^2 + \dfrac{1}{2}m v_2^2 \\\ {u^2} = v_1^2 + v_2^2.......\left( 3 \right) \\\$
Now, squaring and adding equation (1) and (2),

$${u^2} + {0^2} = {\left( {{v_1}\cos \theta + {v_2}\cos \phi } \right)^2} + {\left( {{v_1}\sin \theta - {v_2}\sin \phi } \right)^2} \\\ {u^2} = v_1^2{\cos ^2}\theta + v_2^2{\cos ^2}\phi + 2{v_1}{v_2}\cos \theta \cos \phi + v_1^2{\sin ^2}\theta + v_2^2{\sin ^2}\phi - 2{v_1}{v_2}\sin \theta \sin \phi \\\ {u^2} = v_1^2\left( {{{\sin }^2}\theta + {{\cos }^2}\theta } \right) + v_2^2\left( {{{\sin }^2}\phi + {{\cos }^2}\phi } \right) + 2{v_1}{v_2}\left( {\cos \theta \cos \phi - \sin \phi \sin \theta } \right) \\\ {u^2} = v_1^2 + v_2^2 + 2{v_1}{v_2}\cos \left( {\theta + \phi } \right) \\\$$

Now, substituting the values from equation (3),

$$v_1^2 + v_2^2 = v_1^2 + v_2^2 + 2{v_1}{v_2}\cos \left( {\theta + \phi } \right) \\\ 2{v_1}{v_2}\cos \left( {\theta + \phi } \right) = 0 \\\ \cos \left( {\theta + \phi } \right) = 0 \\\ \theta + \phi = {90^ \circ } \\\$$

So, they will move perpendicular to each other

Hence, the correct option is D.

Note: We know that whenever there is movement in the body, the body should have momentum and vice versa. Momentum is the multiplication of the mass and velocity. Now, we know that the second sphere has zero momentum before collision. Now, after the collision the second will get some movement and hence, it experiences momentum. So, by momentum conservation we can solve this question easily.