Question

When three resistors connected in a parallel arrangement to a battery, then the
(A) Current will be the same through each resistor.
(B) current will be different through each resistor.
(C) potential will be the same across each resistor.
(D) potential will be different across each resistor.
(This question has multiple correct options)

Answer 1

Consider three resistances connected in parallel combination. The group will have two endpoints. Connect a battery of certain voltage across these two ends. Now use laws related to currents and voltages in circuits which are known to you to obtain a relation between the
resistances, currents in each resistor and the voltage across each resistor.

Complete step by step solution:
Consider a parallel combination of three resistors having endpoints A and B with a battery of EMF
$\xi$ connected as shown on figure.

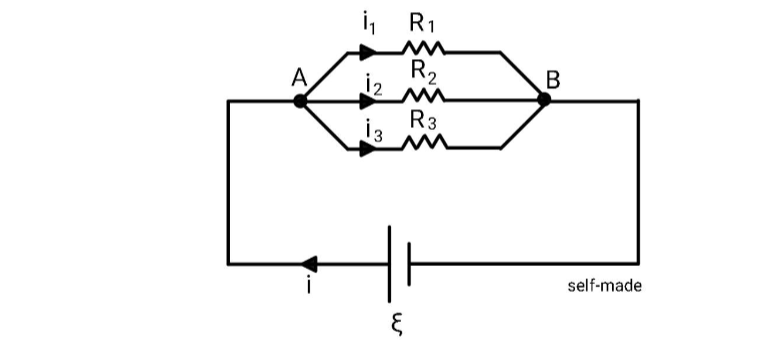
To calculate the potential difference across the resistors, we will use the voltage drop method which
basically gives you the decrease in potential along the path of a current. So, if we go from point A to
point B through the path where the battery is placed, we will have, potential at A plus potential drop
across the battery equals the potential of final destination which is point B. Mathematically,

$
{V_A} + \left( { - \xi } \right) = {V_B} \\

{V_A} - {V_B} = \xi \\
$
Therefore, potential difference between points A and B is equal to the EMF of the battery.

Now, let us consider the resistor ${R_1}$, if you want to find the potential difference across it, you
need to consider the current path along ${R_1}$ which starts from point A, goes through resistor
${R_1}$ and reaches point B. Let the potential across ${R_1}$ be ${V_1}$, by voltage drop method,
we will have, potential at A plus potential drop across ${V_1}$ equals the potential of final
destination which is point B. Mathematically,

$
{V_A} + \left( { - {V_1}} \right) = {V_B} \\
{V_A} - {V_B} = {V_1} \\

$

${V_1} = \xi$. As you can see that the potential across the resistor ${R_1}$ is equal to the EMF of
the battery. Similarly, if you want to find out the potential across ${R_2}$ and ${R_3}$, you will go
use the same method and the same path AB. Eventually you will get to know that the potential
differences across ${R_2}$ and ${R_3}$ will be equal to EMF of the battery. Hence, the potential will
be the same across each resistor.

Now, by Ohm’s Law, we have current as $i = \dfrac{V}{R}$, where $V$ is the potential difference
across the resistor and $R$ is the resistance of the resistor. Since the current through ${R_1}$ is
${i_1}$, we have ${i_1} = \dfrac{{{V_1}}}{{{R_1}}} = \dfrac{\xi }{{{R_1}}}$

Similarly, the currents in the resistors ${R_2}$ and ${R_3}$ will be given as ${i_2} = \dfrac{\xi }{{{R_2}}}$ and ${i_3} = \dfrac{\xi }{{{R_3}}}$ respectively. As you can see that the current in
resistors depend on the resistances. So, in general the current is different. But if the resistances of
the three resistors are the same, the current through each resistor will be the same. So, we cannot
say about the equality of the currents in each resistor, but we can surely say that the potential
across each resistor will be the same.

Hence, when three resistors are connected in a parallel arrangement to a battery, then the potential
will be the same across each resistor.

Hence, the Option (C) is correct.

Note: Remember the laws related to the currents, voltages and resistances in a circuit, such as
Ohm’s Law, Kirchoff’s Law and the loop law. Using these you can find relations between the above
mentioned quantities. Also remember that, whenever resistors are connected in parallel, the
potential across them will be equal and when resistors are in series, the current the resistors
connected in series will be the same.