Question

When three capacitors of equal capacities are connected in parallel and one of the same capacity is connected in series with its combination. The resultant capacity is $3.75\mu F$ . The capacity of each capacitor is:
A) $5\mu F$
B) $6\mu F$
C) $7\mu F$
D) $8\mu F$

Answer 1

For capacitors connected in parallel, the resultant capacity is the arithmetic sum of each capacitor. For capacitors connected in series, the resultant capacity is the sum of the inverses of each capacitor. Draw a labelled diagram and solve accordingly.

Complete step by step solution:
A capacitor is a device which stores the electrical energy in its electric field. It is a passive electronic component with two terminals (passive electronic components do not generate energy). The effect of a capacitor is known as capacitance.
Let the capacitance of each capacitor be $C$. Let ${C_1}, {C_2}, {C_3} and {C_4}$ be the four capacitors that have capacitances as follows.

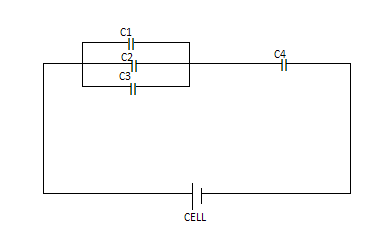
${C_1} = {C_2} = {C_3} = {C_4} = C$ . As all the capacitors are given to be of equal capacitances.
Now as capacitors are connected in parallel and we know that when capacitors are connected in parallel then the resultant capacitance is the arithmetic sum of the capacitances.
Therefore the resultant capacitance will be given as:
$\Rightarrow {{C}_{0}}=C+C+C$
$\Rightarrow {{C}_{0}}=3C$
Now one capacitor is in series and for series combination the resultant will be given as follows
$\Rightarrow \dfrac{1}{{{C}_{final}}}=\dfrac{1}{3C}+\dfrac{1}{C}$
$\Rightarrow \dfrac{1}{3.75}=\dfrac{1}{3C}+\dfrac{1}{C}$
Solving this we get
$\Rightarrow C=5$

Therefore the value of each capacitor is $5\mu F$ . Hence Option $A$ is correct.

Note: Don’t confuse resistors. While calculating resultant resistance, for series combination the resultant resistance is the arithmetic sum of individual resistances but in capacitors it is reverse of resistances. The capacitance of a given circuit is increased by connecting the capacitors in parallel. Similarly the capacitance of a given circuit is decreased by connecting the capacitors in series with respect to each other.