Question

When the switch $S$ , in the circuit shows, is closed, then the value of current $i$ will be:

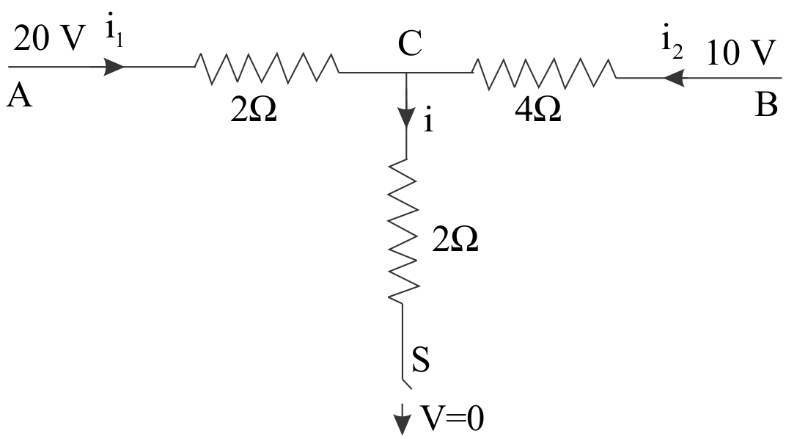
(A) $3A$
(B) $5A$
(C) $4A$
(D) $2A$

Answer 1

Let the potential across terminal C be $xV$ and apply the Kirchoff’s Current Law at point C i.e. the current incoming is equal to the current outgoing . And first find the value of $x$ and this will ultimately help us in finding the value of $i$ .

Complete step by step solution:

One end of the terminal C is grounded as we can clearly see and it has a potential of zero volts. As soon as the switch is closed the current will start running in that arm and we are required to find that value .
Let the potential at point C be $xV$ .
At point C , we will apply Kirchoff’s First Law or we can say Kirchoff’s Current law which states that: the sum of currents entering the junction is equal to the sum of currents leaving the junction . It is based on the principle of conservation of charge.
This means that: $i = {i_1} + {i_2}$ ……..(i)
We know from Ohm’s Law that -

$$current = \dfrac{{voltage}}{ resistor \\\ \\\ } \\\ i = \dfrac{V}{R} \\\$$

Writing the respective values of $i,{i_1},{i_2}$ in eq(i) in terms of voltage and resistance across them .

$$i = {i_1} + {i_2} \\\ \dfrac{{x - 0}}{2} = \dfrac{{20 - x}}{2} + \dfrac{{10 - x}}{4} \\\ 2x = (40 - 2x) + (10 - x) \\\ 2x + 2x + x = 50 \\\ 5x = 50 \\\ x = 10V \\\$$

Now we know that-

$$i = \dfrac{{x - 0}}{2} \\\ i = \dfrac{{10}}{2} \\\ i = 5A \\\$$

Hence, the correct option is B.

Note: We have to keep in mind that we have taken $x$ as the potential across C and not potential drop ( which is the difference in potential between two points) while in the ohm’s law we always take potential difference across any two terminals . So that is why while writing the values of current we have written potential differences.