Question

When the object is at distances ${{u}_{1}}$ and ${{u}_{2}}$ the images formed by the same lens are real and virtual respectively and of the same size. Then focal length of the lens is:

& \text{A}\text{. }\dfrac{1}{2}\sqrt{{{u}_{1}}{{u}_{2}}} \\\ & \text{B}\text{. }\dfrac{1}{2}\left( {{u}_{1}}+{{u}_{2}} \right) \\\ & \text{C}\text{. }\sqrt{{{u}_{1}}{{u}_{2}}} \\\ & \text{D}\text{. 2}\left( {{u}_{1}}+{{u}_{2}} \right) \\\ \end{aligned}$$

Answer 1

In the question an object is kept in front of the same lens at two different distances. One time the image formed is real and the other time the image is virtual. Using the lens formula we can find the distance at which the image is formed and using the magnification formula we can find the magnification of the images. Since the images formed during both cases are of the same size we can equate magnification and thus we get the focal length of the lens.

Formula used: Lens formula, $\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$
Magnification,
$\begin{aligned} & m=\dfrac{I}{O} \\\ & \Rightarrow m=\dfrac{v}{u} \\\ \end{aligned}$

Complete step by step solution:
In the question a convex lens is given and an object is kept at ${{u}_{1}}$ and ${{u}_{2}}$
It is said that when the object is kept at ${{u}_{1}}$ the image formed is real and when it is kept at ${{u}_{2}}$ the image formed is virtual.

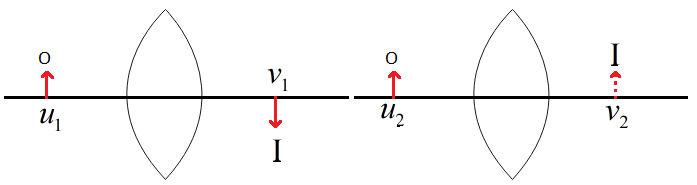
The situations are shown in the figure above.
When the object is kept at ${{u}_{1}}$ the real image is formed at ${{v}_{1}}$ and when the object is kept at ${{u}_{2}}$ the virtual image is formed at ${{v}_{2}}$.
We know the lens formula,
$\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$, were ‘v’ is the distance were image is formed, ‘u’ is the distance were object is kept and ‘f’ is the focal length of the lens.
From the above equation we can find ‘v’ as,
$v=\dfrac{uf}{u+f}$
We also know the equation for magnification,
$\begin{aligned} & m=\dfrac{I}{O} \\\ & \Rightarrow m=\dfrac{v}{u} \\\ \end{aligned}$
Here ‘m’ is the magnification, ‘I’ is where the image is formed i.e. ‘v’ and ‘O’ is where the object is kept i.e. ‘u’.
Let us consider the situation when object is at ${{u}_{1}}$, i.e. when real image is formed, we get magnification as,
${{m}_{1}}=\dfrac{{{v}_{1}}}{{{u}_{1}}}$
We know that for a real image the magnification will always be negative.
Therefore,
${{m}_{1}}=-\dfrac{{{v}_{1}}}{{{u}_{1}}}$
From earlier calculations we have, $v=\dfrac{uf}{u+f}$
Therefore ${{v}_{1}}$ can be written as,
${{v}_{1}}=\dfrac{{{u}_{1}}f}{{{u}_{1}}+f}$
Hence the magnification of real image will become,
${{m}_{1}}=-\left( \dfrac{\dfrac{{{u}_{1}}f}{{{u}_{1}}+f}}{{{u}_{1}}} \right)$
$\Rightarrow {{m}_{1}}=\dfrac{-f}{{{u}_{1}}+f}$
Now let us consider the situation when the object is kept at ${{u}_{2}}$ , i.e. when the image is virtual, we have magnification as,
${{m}_{2}}=\dfrac{{{v}_{2}}}{{{u}_{2}}}$
Since magnification of virtual images is always positive, the above equation remains the same.
We have ${{v}_{2}}=\dfrac{{{u}_{2}}f}{{{u}_{2}}+f}$
Therefore the magnification for virtual image,
${{m}_{2}}=\left( \dfrac{\dfrac{{{u}_{2}}f}{{{u}_{2}}+f}}{{{u}_{2}}} \right)$
$\Rightarrow {{m}_{2}}=\dfrac{f}{{{u}_{2}}+f}$
In the question it is said that the image formed during the two situations is the same, i.e. the magnification is the same.
Hence we can equate the magnification of virtual image and real image, i.e.
${{m}_{1}}={{m}_{2}}$
$\Rightarrow \dfrac{-f}{{{u}_{1}}+f}=\dfrac{f}{{{u}_{2}}+f}$
$\Rightarrow -\left( {{u}_{2}}+f \right)={{u}_{1}}+f$
$\Rightarrow -{{u}_{2}}-f={{u}_{1}}+f$
$\Rightarrow 2f=-{{u}_{2}}-{{u}_{1}}$
$\Rightarrow 2f=-\left( {{u}_{1}}+{{u}_{2}} \right)$
$\Rightarrow f=-\dfrac{1}{2}\left( {{u}_{1}}+{{u}_{2}} \right)$
Thus we get the focal length of the lens as $\left( -\dfrac{1}{2}\left( {{u}_{1}}+{{u}_{2}} \right) \right)$. But we know that for a real image and a virtual image, the object distance is taken as negative, i.e. in this case,
${{u}_{1}}=-{{u}_{1}}$
${{u}_{2}}=-{{u}_{2}}$
By applying this sign convention in the obtained focal length equation, we get
$\Rightarrow f=-\dfrac{1}{2}\left( -{{u}_{1}}-{{u}_{2}} \right)$
$\Rightarrow f=-\dfrac{1}{2}\times -\left( {{u}_{1}}+{{u}_{2}} \right)$
$\Rightarrow f=\dfrac{1}{2}\left( {{u}_{1}}+{{u}_{2}} \right)$
Therefore the focal of the lens is $\dfrac{1}{2}\left( {{u}_{1}}+{{u}_{2}} \right)$.

So, the correct answer is “Option B”.

Note: A real image is formed when a ray of light from a light beam converges. The real image formed by the converging of light will always be inverted. This is why we take the magnification of a real image as negative.
In case of a virtual image it is formed due to the diverging of the light rays, i.e. virtual image is formed due to the imaginary intersection of light rays. A virtual image will always be upright and hence we take the magnification of a virtual image as negative.