Question
Question: When the left arm of a mercury manometer is connected to a cylinder filled with a gas , the level of...
When the left arm of a mercury manometer is connected to a cylinder filled with a gas , the level of the mercury in the right arm rises by 2 mm. If the pressure of the gas in the container is 110160 Pa, the atmospheric pressure is ………… cm of Hg. ( take g=10ms−2 )
A. 79
B. 85
C. 76
D. 81
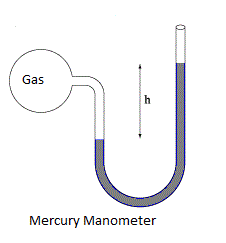
Solution
Finding the value of atmospheric pressure, pressure of gas is balanced with atmospheric pressure and pressure due to rise in mercury manometer.
Complete step-by-step solution: Mercury Manometer left arm is attached to a gas pipe and mercury level rises by 2 mm in the right arm as you can see in the diagram of mercury manometer.
We have pressure of gas in the container 110160 Pa. For finding the pressure of the atmosphere, balance the pressure of the left arm with the pressure of the right arm of the mercury manometer. Let atmospheric pressure is Pa , pressure due to rise in level of mercury in the right arm PHg and pressure due to gas in the container PG .
Now, we balance the pressure of the left arm and right arm then we find that the pressure of gas is equal to atmospheric pressure and pressure due to rise in mercury level in the right arm.
⇒PG=Pa+PHg ⋯⋯⋯ equation (1)
Now, we calculate PHg and we know that pressure is equal to the product of density, gravity acceleration and height of liquid.
⇒PHg=ρHg×g×h
We know that density of Mercury (ρHg) =13.56 gcm−3 , gravity acceleration (g)=10ms−2 and rise in mercury level h=4 mm due to fall in left arm by 2 mm and rise in right arm by 2mm. Put these values on above equation to get pressure of mercury,
⇒PHg=13.56×1000×104 (∵10ms−2=1000cms−2)
⇒PHg=5424 Pa (∵4mm=104cm)
Now, putting value of pressure of gas PG , pressure due to rise in mercury PHg in equation (1)
⇒110160=Pa+5424
⇒Pa=110160−5424
Now, we get
⇒Pa=104736 Pa
We know that 1cm of Hg =1333 Pa. So, we divide the atmospheric pressure by 1333 to get the pressure in cm of Hg.
⇒Pa=1333104736
⇒Pa= 78.57≈79 cm of Hg
Hence, option (A) is correct.
Note:- Pressure is also defined as force exerted in unit area. Pressure can be classified as gauge pressure, atmospheric pressure and absolute pressure.
