Question

When the current in the portion of the circuit shown in the figure is $2\;{\text{A}}$ and increasing at rate of $1\;{\text{A/s}}$, the measured potential difference ${V_{ab}} = 8\;V$. However when the current is $2\;{\text{A}}$ and increasing at the rate of $1\;{\text{A/s}}$, The measured potential difference ${V_{ab}} = 4\;V$. The values of ${\text{R}}$ and ${\text{L}}$ are:

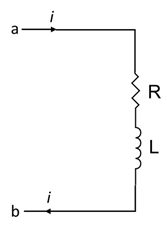
A) $3\;\Omega$ and $2\;{\text{H}}$ respectively.
B) $3\;\Omega$ and $3\;{\text{H}}$ respectively.
C) $2\;\Omega$ and $1\;{\text{H}}$ respectively.
D) $3\;\Omega$ and $1\;{\text{H}}$ respectively.

Answer 1

In this question, use the Kirchhoff’s law to calculate the values of resistance and the inductance of the circuit. According to Kirchhoff's law potential difference is equal to the product of current and resistance and sum of the inductance.
Complete step by step answer:
Let us consider figure (1), we have given a circuit with current of $2\;{\text{A}}$ and increasing at rate of $1\;{\text{A/s}}$, the measured potential difference ${V_{ab}} = 8\;V$. And when the current is $2\;{\text{A}}$ is decreasing at the rate of $1\;{\text{A/s}}$ the measured potential difference ${V_{ab}} = 4\;V$.
As we know, Kirchhoff’s law states that the current flowing inside the circuit and outside the circuit will be the same. Kirchhoff’s law is also known as the conservation law of the current.
Now, we calculate the value for the potential difference as,
$\Rightarrow {V_A} - IR - L\dfrac{{dI}}{{dt}} = {V_b}$
After simplification we get,
$\Rightarrow {V_A} - {V_b} = IR + L\dfrac{{dI}}{{dt}}$
Now we substitute the value of current and the potential difference,
$8 = 2R + L\left( 1 \right)$
Simplify the equation and we get
$8 = 2R + L......\left( 1 \right)$
Simplify the above equation again and get,
$\Rightarrow \dfrac{{8 - L}}{2} = R$
Now, we calculate the value for the potential difference ${V_{ab}} = 4\;V$
$\Rightarrow {V_A} - IR - L\dfrac{{dI}}{{dt}} = {V_b}$
After simplification we get,
$\Rightarrow {V_A} - {V_b} = IR + L\dfrac{{dI}}{{dt}}$
Now, we substitute the value of current and the potential difference,
$\Rightarrow 4 = 2R + L\left( { - 1} \right)$
Simplify the equation and we get
$\Rightarrow 4 = 2R - L$
Put the value of $R$ in equation in the above equation,
$\Rightarrow 4 = 2\left( {\dfrac{{8 - L}}{2}} \right) - L$
After simplification we get,
$\therefore L = 2\;{\text{H}}$

Now, we substitute the value of $L$ in equation $\left( 1 \right)$
$\Rightarrow 8 = 2R + 2$
After simplification we get,
$\therefore R = 3\;\Omega$
Therefore, The value of ${\text{R}}$ is $3\;\Omega$ and the value of ${\text{L}}$ is $2\;{\text{H}}$.

So, the option $\left( A \right)$ is correct.

Note: In this question, do not forget to write the SI unit of the frequency. And the SI unit of the inductance is Henry$\left( {\text{H}} \right)$.Conservation of the current law means the current inside and outside is the same.