Question

When $\sin x=0$ what does x equal?

Answer 1

In order to determine the solution, first of all we need to know the value of sin in such a way that expression should be 0. But as we know that sin is also known as a periodic function that oscillates at a regular interval that is 0. At $x=0,\,\pi ,\,2\pi$ in the domain.

Complete step-by-step solution:
We have given the trigonometry equation $\sin x=0$. In this equation, we have to find the values of x.
The given expression is $\sin x=0$
If you see in this expression then sin is also known as periodic function that oscillates at regular interval and it crosses the x axis (that is 0) at $x=0,\,\pi$ and $2\pi$ in the domain $\left[ 0,2\pi\right]$ and it continues to cross the x axis at every integer multiple of $\pi$
For more understanding clearly figure is given below:

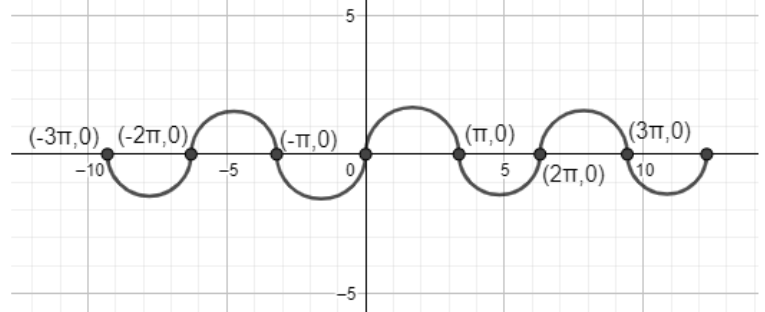
Range of this above graph is given below that is
Graph $\left( \sin x\left[ -1,1 \right] \right)$
So whenever $\sin x=0$ , we have that
$x=\pi \pm k\pi$ For all values of k in the set of integers.
That means we can consider the value of k as if $k=0,1,2,.........N$ where N is some arbitrary large integer.
Then $\sin x=0$ for $x=0,\pm \pi ,\pm 2\pi ,......\pm 2N\pi$

Note: One must be careful while taking values from the trigonometry table and cross check at least once to avoid error in the answer. If you put a multiple of $2\pi$ that is $2N\pi$ where N is a larger integer value then also the expression becomes 0. In this question, students can also check the values of x in the equation given in the question and if the solution comes as 0 then, the values of x are correct.