Question

When N₂(g) and H₂(g) are mixed N₂H₄ (g), NH₃(g) or both may form, depending upon the relative amount of N₂ and H₂ taken. If initial moles of N₂, H₂ are x, y and final moles of N₂H₄, NH₃ are z, v, then the correct options from the following in order of (x, y, z, v) is/are -

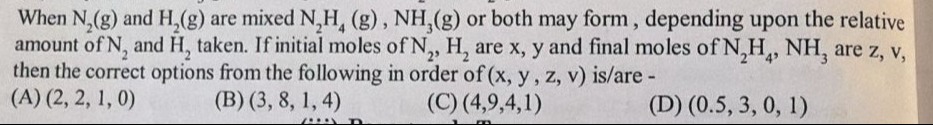
• A. (2, 2, 1, 0)
• B. (3, 8, 1, 4)
• C. (4,9,4,1)
• D. (0.5, 3, 0, 1)

Answer 1

Answer: (A), (B), (D)

(A), (B), (D)

Answer 2

The reactions that can occur are:

1. N₂(g) + 2H₂(g) $\rightarrow$ N₂H₄(g)
2. N₂(g) + 3H₂(g) $\rightarrow$ 2NH₃(g)

Let the initial moles of N₂ be $x$ and H₂ be $y$. Let the final moles of N₂H₄ be $z$ and NH₃ be $v$.

Let the moles of N₂ consumed to form N₂H₄ be $z$.
Let the moles of H₂ consumed to form N₂H₄ be $2z$.
Let the moles of N₂ consumed to form NH₃ be $v/2$.
Let the moles of H₂ consumed to form NH₃ be $3v/2$.

The total moles of N₂ consumed = $z + v/2$.
The total moles of H₂ consumed = $2z + 3v/2$.

For the final state to be reachable from the initial state, the amount of reactant consumed cannot exceed the initial amount of the reactant. So, we must have:

Initial moles of N₂ $\ge$ Moles of N₂ consumed $\implies x \ge z + v/2$
Initial moles of H₂ $\ge$ Moles of H₂ consumed $\implies y \ge 2z + 3v/2$

We also need to check the conservation of atoms.

Initial number of N atoms = $2x$
Initial number of H atoms = $2y$
Final number of N atoms = $2 \times (\text{final moles of N₂H₄}) + 1 \times (\text{final moles of NH₃}) + 2 \times (\text{final moles of N₂})$
Final number of H atoms = $4 \times (\text{final moles of N₂H₄}) + 3 \times (\text{final moles of NH₃}) + 2 \times (\text{final moles of H₂})$

Let the final moles of N₂ be $x_f$ and H₂ be $y_f$.

$x_f = x - (z + v/2)$
$y_f = y - (2z + 3v/2)$

Since the final amounts cannot be negative, $x_f \ge 0$ and $y_f \ge 0$. These are the same as the conditions derived from reactant consumption.

Let's check each option:

(A) (x, y, z, v) = (2, 2, 1, 0)

$x = 2, y = 2, z = 1, v = 0$

Check conditions:

$x \ge z + v/2 \implies 2 \ge 1 + 0/2 \implies 2 \ge 1$ (True)
$y \ge 2z + 3v/2 \implies 2 \ge 2(1) + 3(0)/2 \implies 2 \ge 2 + 0 \implies 2 \ge 2$ (True)

Moles of N₂ consumed = $1 + 0/2 = 1$. Remaining N₂ = $2 - 1 = 1$.
Moles of H₂ consumed = $2(1) + 3(0)/2 = 2$. Remaining H₂ = $2 - 2 = 0$.

Final state: 1 mole N₂H₄, 0 moles NH₃, 1 mole N₂, 0 moles H₂.

Initial N atoms = $2(2) = 4$. Final N atoms = $2(1) + 1(0) + 2(1) = 4$. (Conserved)
Initial H atoms = $2(2) = 4$. Final H atoms = $4(1) + 3(0) + 2(0) = 4$. (Conserved)

Option (A) is consistent.

(B) (x, y, z, v) = (3, 8, 1, 4)

$x = 3, y = 8, z = 1, v = 4$

Check conditions:

$x \ge z + v/2 \implies 3 \ge 1 + 4/2 \implies 3 \ge 1 + 2 \implies 3 \ge 3$ (True)
$y \ge 2z + 3v/2 \implies 8 \ge 2(1) + 3(4)/2 \implies 8 \ge 2 + 6 \implies 8 \ge 8$ (True)

Moles of N₂ consumed = $1 + 4/2 = 3$. Remaining N₂ = $3 - 3 = 0$.
Moles of H₂ consumed = $2(1) + 3(4)/2 = 2 + 6 = 8$. Remaining H₂ = $8 - 8 = 0$.

Final state: 1 mole N₂H₄, 4 moles NH₃, 0 moles N₂, 0 moles H₂.

Initial N atoms = $2(3) = 6$. Final N atoms = $2(1) + 1(4) + 2(0) = 2 + 4 = 6$. (Conserved)
Initial H atoms = $2(8) = 16$. Final H atoms = $4(1) + 3(4) + 2(0) = 4 + 12 = 16$. (Conserved)

Option (B) is consistent.

(C) (x, y, z, v) = (4, 9, 4, 1)

$x = 4, y = 9, z = 4, v = 1$

Check conditions:

$x \ge z + v/2 \implies 4 \ge 4 + 1/2 \implies 4 \ge 4.5$ (False)

Option (C) is inconsistent because it requires more N₂ than initially available.

(D) (x, y, z, v) = (0.5, 3, 0, 1)

$x = 0.5, y = 3, z = 0, v = 1$

Check conditions:

$x \ge z + v/2 \implies 0.5 \ge 0 + 1/2 \implies 0.5 \ge 0.5$ (True)
$y \ge 2z + 3v/2 \implies 3 \ge 2(0) + 3(1)/2 \implies 3 \ge 0 + 1.5 \implies 3 \ge 1.5$ (True)

Moles of N₂ consumed = $0 + 1/2 = 0.5$. Remaining N₂ = $0.5 - 0.5 = 0$.
Moles of H₂ consumed = $2(0) + 3(1)/2 = 1.5$. Remaining H₂ = $3 - 1.5 = 1.5$.

Final state: 0 moles N₂H₄, 1 mole NH₃, 0 moles N₂, 1.5 moles H₂.

Initial N atoms = $2(0.5) = 1$. Final N atoms = $2(0) + 1(1) + 2(0) = 1$. (Conserved)
Initial H atoms = $2(3) = 6$. Final H atoms = $4(0) + 3(1) + 2(1.5) = 0 + 3 + 3 = 6$. (Conserved)

Option (D) is consistent.

All options (A), (B), and (D) are consistent with the conservation of mass and the stoichiometry of the reactions.