Question: When it rains vertically down, to a man walking on road the velocity of rain appears to be 1.5 times...

Question

When it rains vertically down, to a man walking on road the velocity of rain appears to be 1.5 times his velocity. To protect himself from rain he should hold the umbrella at $\theta$ vertical. Then $\tan \theta$
$\begin{aligned} & (A)\dfrac{2}{\sqrt{5}} \\\ & (B)\dfrac{\sqrt{5}}{2} \\\ & (C)\dfrac{2}{3} \\\ & (D)\dfrac{3}{2} \\\ \end{aligned}$

Answer 1

Solution

Take the direction of man in x-axis and velocity of rain in y-axis. Given that velocity of rain with respect to man is 1.5 times the velocity of man. If the velocity of man is $+{{V}_{m}}$ along positive x-axis, then velocity of man in negative x-axis is $-{{V}_{m}}$ .And theta be the angle between ${{V}_{rm}}$ and ${{V}_{r}}$ . Then calculate sine of that angle. After calculating the sine of angle, consider a right angled triangle and calculate the third side of the triangle. From that find the value of $\tan \theta$ .

Complete answer:
Let ${{V}_{m}}$ be the velocity of man and ${{V}_{r}}$ be the velocity of rain.
Also given that velocity of rain with respect to man is,
${{V}_{rm}}=1.5{{V}_{m}}$
$\Rightarrow {{V}_{rm}}={{V}_{r}}-{{V}_{m}}$

Thus,
$\sin \theta =\dfrac{{{V}_{m}}}{1.5{{V}_{m}}}$
Cancelling ${{V}_{m}}$ we get,
$\Rightarrow \sin \theta =\dfrac{1}{1.5}$
$\Rightarrow \sin \theta =\dfrac{1}{\dfrac{3}{2}}$
$\Rightarrow \sin \theta =\dfrac{2}{3}$
Consider a right angled triangle ABC,

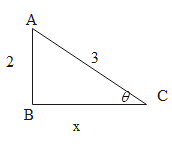
Here we have to find BC.
So by applying Pythagoras theorem we get,
$B{{C}^{2}}={{(AC)}^{2}}-{{(AB)}^{2}}$
$\Rightarrow B{{C}^{2}}={{3}^{2}}-{{2}^{2}}=5$
$\Rightarrow BC=\sqrt{5}$
Hence,
$\tan \theta =\dfrac{AB}{BC}$
$\Rightarrow$ $\tan \theta =\dfrac{2}{\sqrt{5}}$

So, the correct answer is “Option A”.

Note:
Velocity of rain with respect to the man is the difference in velocity of rain to the velocity of man.
This type of velocity is known as the relative velocity, which compares the velocity of one object with respect to another one. While considering relative motion between two objects, one is considered to be in the state of rest and other will be in the state of motion.