Question

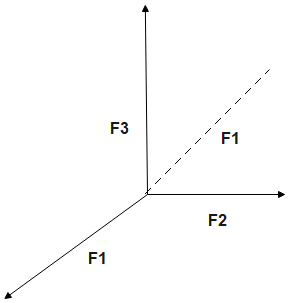
When forces $\mathbf{F}_{1}, \mathbf{F}_{2}, \mathbf{F}_{3}$ are acting on a particle of mass $\mathbf{m}$ such that $\mathbf{F}_{2}$ and $\mathbf{F}_{3}$ are mutually perpendicular, then the particle remains stationary. If the force $\mathbf{F}_{1}$ is now removed then the acceleration of particle the is
A. $\dfrac{{{\text{F}}_{1}}}{m}$
B. $\dfrac{{{\text{F}}_{2}}~{{\text{F}}_{3}}}{\text{m}{{\text{F}}_{1}}}$
C. $\dfrac{\left( {{\text{F}}_{2}}-{{\text{F}}_{3}} \right)}{\text{m}}$
D.$\dfrac{{{\text{F}}_{2}}}{m}$

Answer 1

As the issue that particles are stationary is given, then zero will be the result of the forces. We can find the value of force from the relation of the resulting forces. Now, we will use Newton's law of motion equation, which is given below, to calculate the acceleration of the particle.
Formula used:

The equation of Newton's second law of motion is given below
$F=m a$
$\Rightarrow a=\dfrac{F}{m}$
Here, $F$ is the force acting on the particle, $m$ is the mass of the particle and $a$ is the acceleration of the particle.

Complete answer:
Consider a particle of mass $m$ on which three forces $F_{1}, F_{2}$ and $F_{3}$ are acting. Now, when the particle remains
stationary, then the resultant of the three forces will be zero and is given below
$F_{1}+F_{2}+F_{3}=0$
$\Rightarrow F_{1}=-\left(F_{2}+F_{3}\right)$
Therefore, from the above relation, we can say that the magnitude of force $F_{1}$ is equal to the magnitude of the sum of
forces $F_{2}$ and $F_{3}$ i.e. $F_{2}+F_{3},$ but the direction of these forces $F_{2}+F_{3}$ will be opposite to force $F_{1} .$ Now, consider
that the force $F_{1}$ is now removed from the particle of mass $m$, therefore, the magnitude of the force of particle acting
on the mass $m$ will be
$\Rightarrow$ magnitude of $\left(F_{2}+F_{3}\right)$
$\Rightarrow-$ magnitude of $F_{1}$
Now, according to Newton's second law of motion, the acceleration of the particle can be calculated as shown below
$F=m a$
$\Rightarrow a=\dfrac{F}{m}$
Therefore, the acceleration of particle in case of magnitude of force when $F_{1}$ is removed is given below
$a=\dfrac{F_{2}+F_{3}}{m}$
$\therefore a=\dfrac{{{F}_{1}}}{m}$
Therefore, the magnitude of acceleration of the particle is $-\dfrac{F_{1}}{m},$ but the direction of acceleration is opposite to the force $F_{1}$.

Correct option is (A).

Note:
Here, we've got the negative value of acceleration. When the moving object slows down, the acceleration of the particle will be negative. We can also say that when the particle's speed decreases, the acceleration of the particle will be negative.