Question

When an unknown resistance and a resistance of 4Ω are connected in the left and right gap of a meter bridge, the balance point is obtained at 50cm. The shift in the balance point, if a 4Ω resistance is now connected in parallel to the resistance in the right gap, is
A. 66.7 cm
B. 16.7 cm
C. 34.6 cm
D. 14.6 cm

Answer 1

In this question, a balance point is given for an unknown resistance and a known resistance, which is the shifted due to the addition of resistance in parallel to a known resistance of 4Ω in the right gap, hereby using the meter bridge resistance and the length formula we will first find unknown resistance than the new balance point.

Complete step by step answer: An unknown resistance is connected in the left gap of the meter bridge
Resistance connected in the right gap of the meter bridge=4Ω
Let the unknown resistance be $R$

We know in a meter bridge, the ratio of the resistances is directly proportional to the length, which is given as
$\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{l_1}}}{{100 - {l_1}}} - - (i)$
Hence we can write equation (i) as

$$\dfrac{R}{4} = \dfrac{{50}}{{100 - 50}} \\\ \Rightarrow \dfrac{R}{4} = \dfrac{{50}}{{50}} \\\ \Rightarrow \dfrac{R}{4} = 1 \\\ \Rightarrow R = 4\Omega - - (ii) \\\$$

So the value of unknown resistance will be equal to$= 4\Omega$
Now it is said that resistance of 4Ω is now connected in parallel to the resistance in the right gap,
So the equivalent resistance in the right gap will become

$$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_{4\Omega }}}} + \dfrac{1}{{{R_{4\Omega }}}} \\\ \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{4} + \dfrac{1}{4} \\\ \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{2}{4} \\\ \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{2} \\\$$

Therefore the new value of resistance in the right gap will be $= 2\Omega$

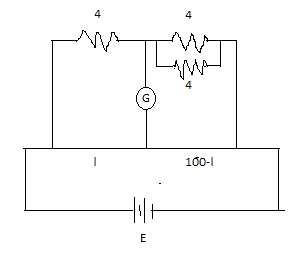
Now let’s find the new balance point after shifting by using equation (i)
$\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{l_1}}}{{100 - {l_1}}} - - (i)$
By substituting the values, we get

$$\Rightarrow \dfrac{{{R_1}}}{{{R_{equ}}}} = \dfrac{{{l_2}}}{{100 - {l_2}}} \\\ \Rightarrow \dfrac{4}{2} = \dfrac{l}{{100 - l}} \\\ \Rightarrow 4\left( {100 - l} \right) = 2l \\\ \Rightarrow 400 = 2l + 4l \\\ \Rightarrow 6l = 400 \\\ \Rightarrow l = 66.67cm \\\$$

Therefore the new balance point after shifting will be at $= 66.7cm$
Option A is correct.

Note: Students must note that the meter bridge works on the principle of Wheatstone bridge, where the null point is found by moving the pointer. Moreover, it should be noted here that the additional resistance has been connected in parallel and not in series, if it would be connected in series then, the equivalent resistance would be 8 ohms.