Question

When an object is shot from the bottom of a long smooth inclined plane kept at an angle ${{60}^{\circ }}$ with horizontal, it can travel a distance ${{x}_{1}}$ along the plane. But when the inclination is decreased to ${{30}^{\circ }}$ and the same object is shot with the same velocity, it can travel ${{x}_{2}}$ distance. Then ${{x}_{1}}:{{x}_{2}}$ will be:
A) $1:2\sqrt{3}$
B) $1:\sqrt{2}$
C) $\sqrt{2}:1$
D) $1:\sqrt{3}$

Answer 1

Draw free body diagram of the system. Take the components of acceleration in the direction of motion. The initial velocity and time is not given. Use kinematical equations accordingly.

Complete step by step solution:
The problem is that of a body on an inclined plane. It will be easier to draw the Free Body Diagram and denote the forces. Since force is a vector quantity hence it is necessary to denote the direction of the force in the free body diagram.

Consider the free body diagram below:

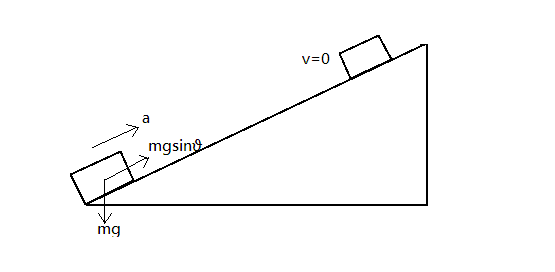
Here, $mg$ is the force applied on body of mass $m$
$mg\sin \theta$ is the component of force in the direction denoted by arrow and
$-mg\sin \theta$ taking the component to $mg\sin \theta$ in the opposite direction.
$a$ Represents the direction in which the object is accelerated.
$v=0$ Represent that the final velocity is equal to zero.
$\theta$ Represent the angle of the smooth plane with the horizontal.
We are required to find the ratio of distance travelled when $\theta ={{60}^{\circ }}$ and $\theta =3{{0}^{\circ }}$.
Since there is no mention of time in the given problem hence we will use the following kinematical equation to find distance travelled by the object.
${{v}^{2}}={{u}^{2}}+2as$
Where $v$ is the final velocity
$u$ Is the initial velocity
$a$ Is the acceleration of the object in the direction of motion
$s$ Is the distance travelled.
As the final velocity is zero hence $v=0$ , substituting this value in above equation
$0={{u}^{2}}+2as$
Here $a=-g\sin \theta$ since the body is moving in the upward direction
$\Rightarrow -{{u}^{2}}=-2s(g\sin \theta )$
$\Rightarrow s=\dfrac{{{u}^{2}}}{2g\sin \theta }$
This is the general equation for any angle.
It is mentioned in the question that for $\theta ={{60}^{\circ }}$ $s={{x}_{1}}$ and for $\theta ={{30}^{\circ }}$ $s={{x}_{2}}$
Put these values in above equation, we get
${{x}_{1}}=\dfrac{{{u}^{2}}}{2g\sin {{60}^{\circ }}}$ AND ${{x}_{2}}=\dfrac{{{u}^{2}}}{2g\sin {{30}^{\circ }}}$
Dividing both the equations we get
$\dfrac{{{x}_{1}}}{{{x}_{2}}}=\dfrac{\sin {{30}^{\circ }}}{\sin {{60}^{\circ }}}$
$\dfrac{{{x}_{1}}}{{{x}_{2}}}=\dfrac{1}{\sqrt{3}}$
Since value of $\sin {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}$ and $\sin {{30}^{\circ }}=\dfrac{1}{2}$

Therefore ${{x}_{1}}:{{x}_{2}}=1:\sqrt{3}$

Option $(D)$ is the correct option.

Note: Force is a vector quantity which means it has magnitude as well as direction. The direction of the force due gravity is always towards the center of Earth. In this particular problem we have neglected the force of friction which always acts in the direction opposite to motion of the object. The initial velocity for the angles will be the same.