Question

When an object is placed on the principal axis of a convex lens at two different positions, it produces the image with magnification +2 and -4 respectively. How many times more away from the lens the image will be formed in the second position as compared to the first position?
A) 2
B) 4
C) 5
D) 10

Answer 1

We have given the magnification of an image from which we can find the relation between the image distance and the distance of the object. Then by using lens formula we can find the relation between the distances of two images formed. As the lens is the same in both conditions the focal length would be the same.

Formula used:

& \dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u} \\\ & m=\dfrac{v}{u} \\\ \end{aligned}$$ **Complete answer:** Let us consider the first case, when the object is placed at distance $${{u}_{1}}$$ from the lens, then the image is formed at $${{v}_{1}}$$ with the magnification +2, the ray diagram for this position can be given as 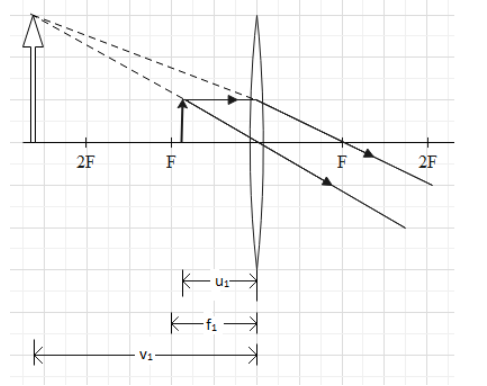 The magnification of the lens is given as $$m=\dfrac{v}{u}$$ In this case value of m is 2 and distance of image from the lens is $${{v}_{1}}$$and distance of object from the lens is$${{u}_{1}}$$, hence we can rewrite the above equation as $$\begin{aligned} & m=\dfrac{{{v}_{1}}}{{{u}_{1}}} \\\ & 2=\dfrac{{{v}_{1}}}{{{u}_{1}}} \\\ & \dfrac{1}{{{u}_{1}}}=\dfrac{2}{{{v}_{1}}}\text{ }...................\text{(i)} \\\ \end{aligned}$$ Now from the lens formula we can write $$\dfrac{1}{{{f}_{1}}}=\dfrac{1}{{{v}_{1}}}-\dfrac{1}{{{u}_{1}}}$$ Where $${{f}_{1}}$$is the focal length of the lens. Substituting the value of $$\dfrac{1}{{{u}_{1}}}$$from equation (i), we get $$\begin{aligned} & \dfrac{1}{{{f}_{1}}}=\dfrac{1}{{{v}_{1}}}-\dfrac{2}{{{v}_{1}}} \\\ & \dfrac{1}{{{f}_{1}}}=-\dfrac{1}{{{v}_{1}}}\text{ }........................\text{(ii)} \\\ \end{aligned}$$ Now considering the second case where an object is placed at distance $${{u}_{2}}$$ from the lens and image is formed at the distance $${{v}_{2}}$$ from the lens with magnification of -4, the ray diagram for this position can be given as 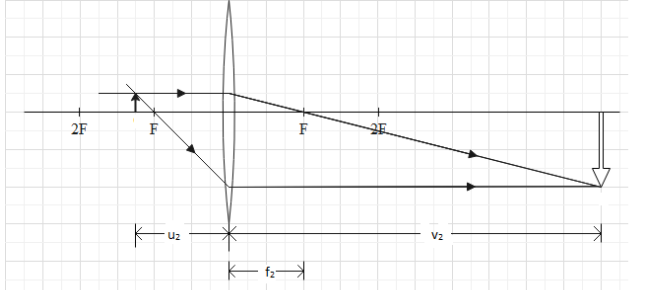 From the magnification formula we can write $$\begin{aligned} & m=\dfrac{{{v}_{2}}}{{{u}_{2}}} \\\ & -4=\dfrac{{{v}_{2}}}{{{u}_{2}}} \\\ & \dfrac{1}{{{u}_{2}}}=-\dfrac{4}{{{v}_{2}}}\text{ }.......................\text{(iii)} \\\ \end{aligned}$$ From the lens formula we can write $$\begin{aligned} & \dfrac{1}{{{f}_{2}}}=\dfrac{1}{{{v}_{2}}}-\dfrac{1}{{{u}_{2}}} \\\ & \\\ \end{aligned}$$ Where $${{f}_{2}}$$is the focal length of the lens. Substituting value of $$\dfrac{1}{{{u}_{2}}}$$from the equation (iii) in the above equation we get $$\begin{aligned} & \dfrac{1}{{{f}_{2}}}=\dfrac{1}{{{v}_{2}}}-\left( -\dfrac{4}{{{v}_{2}}} \right) \\\ & \dfrac{1}{{{f}_{2}}}=\dfrac{1}{{{v}_{2}}}+\dfrac{4}{{{v}_{2}}} \\\ & \dfrac{1}{{{f}_{2}}}=\dfrac{5}{{{v}_{2}}}\text{ }.........................\text{(iv)} \\\ \end{aligned}$$ As per question both the cases have same lens therefore the focal length in both the cases will be same i.e. $${{f}_{1}}={{f}_{2}}$$ Hence equation (ii) and (iv) will be equal and can be rewritten as $$\begin{aligned} & -\dfrac{1}{{{v}_{1}}}=\dfrac{5}{{{v}_{2}}} \\\ & {{v}_{2}}=-5{{v}_{1}} \\\ \end{aligned}$$ Hence, from the above equation we can conclude that the distance of image formed at second position will be 5 times the distance of image formed at first position. **Therefore, option C is the correct answer.** **Note:** The negative sign in the last equation shows that the distance of both the images are measured in opposite directions from the lens. Also note that the negative magnification shows that the image formed will be inverted and real whereas the positive magnification shows that the image is upright and virtual.