Question

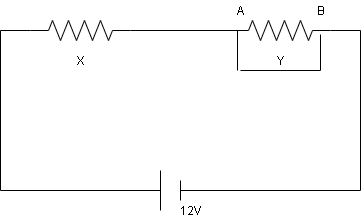
When an ammeter of negligible internal resistance is inserted in series with circuit it reads $1A$. When the voltmeter of very large resistance is connected across X it reads $1V$. When point A and B are shorted by a conducting wire, the voltmeter measures $10V$ across the battery. The internal resistance of the battery is equal to

Answer 1

Recall that there are many laws to calculate voltage around a closed loop. Here, Kirchhoff’s second law will be used. This is also called Kirchhoff’s voltage and current law. This law helps to determine the connection between the elements in the circuits and then evaluates current.

Complete step by step solution:
Step I:
Kirchhoff’s second rule states that the sum of all the electric potential differences around a closed loop is zero. Since there are two resistors connected across the loop and an ammeter is connected in series across the circuit. In any closed loop, the total voltage in the closed-loop is equal to the sum of all the voltage drops connected in the same loop.
Step II:
Current in the circuit, $I = 1A$
The voltage at that time in the circuit, $V = 1V$
Using Ohm’s Law, calculate the resistance as current and voltage is given.
As per Ohm’s Law
$V = IR$---(i)
Substituting the values in equation (i),
$1 = 1 \times R$
$R = \dfrac{1}{1}$
$R = 1\Omega$
Step III:
When the point A and B are shorted by a conducting wire, the voltmeter measures 10V across the battery. Therefore again applying Ohm’s law, given that
$V = 10V$
$R = 1\Omega$
Step IV:
Hence the current is,
$I = \dfrac{V}{R}$---(ii)
Substituting the values in equation (ii)
$I = \dfrac{{10}}{1}$
$I = 10A$
Step V:
Now, the voltage across the terminals of the battery is
$V = E - Ir$
Substituting the values and evaluating the value of ‘r’,
$10 = 12 - 10r$
$10r = 12 - 10$
$10r = 2$
$r = \dfrac{2}{{10}}$
$r = 0.2$

The internal resistance of the battery is $0.2\Omega$.

Note:
Since voltage is a measurement of energy or voltage per unit charge, Kirchhoff’s law follows the Law of conservation of energy. As per this law, the amount of energy gained per unit charge will be equal to the amount of energy lost per unit charge.