Question

When an air column of length l open at both ends produces its fundamental note, the wavelength is given by
$\begin{aligned} & (A)\lambda =l \\\ & (B)\lambda =2l \\\ & (C)\lambda =4 \\\ & (D)\lambda =3l \\\ \end{aligned}$

Answer 1

The mode of vibration in a closed path is in the form of reflection from the closed end. As free ends are free to vibrate, they will have maximum amplitude. As a result of this an antinode is formed at the open end. This can also be described as the simplest mode of vibration and hence it is called the fundamental mode.

Complete answer:
There are a number of natural frequencies set for a musical instrument, which vibrates at the time when a disturbance is introduced to it. The set of natural frequencies are the harmonics of an instrument. There will be a standing wave associated with each of the harmonics.
Each of the modes is associated with a modal frequency and one mode shape. According to the number of half waves, each mode is numbered. The mode of vibration in a closed path is in the form of reflection from the closed end. As free ends are free to vibrate, they will have maximum amplitude. As a result of this an antinode is formed at the open end. This can also be described as the simplest mode of vibration and hence it is called the fundamental mode. Closed pipe shows odd harmonics.

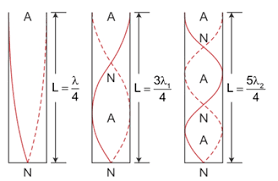
Thus Antinodes are formed at both open ends. $\dfrac{\lambda }{2}$ is the distance between two antinodes.
$\begin{aligned} & \dfrac{\lambda }{2}=l \\\ & \Rightarrow \lambda =2l \\\ \end{aligned}$

Therefore option (B) is correct.

Note:
In a closed path the amplitude will be always minimum. And the amplitude of vibration will be maximum only at the open ends. Thus maximum amplitude forms an antinode, whereas minimum amplitude results in a node. The flute is an instrument with two ends open. Thus antinodes are formed at open end.