Question

When a wire of uniform cross-section $a$ , length $l$ and resistance $R$ is bent into a complete circle, resistance between any two of diametrically opposite points will be:
A. $\dfrac{R}{4}$
B. $\dfrac{R}{8}$
C. $4R$
D. $\dfrac{R}{2}$

Answer 1

We start by writing down the given data and appropriate formulas. We know that if the points are diametrically opposite, the diameter cuts the circle into two semicircles. Then we find the resistance of each semicircle. We then identify the connection of the two resistors and find the equivalent accordingly.

Formulas used:
The equivalent resistance for a parallel connection is given by,
${R_{eq}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$
Where ${R_1}$ and ${R_2}$ are the resistors connected in parallel.

Complete step by step answer:
Let us start by writing down the given information, given that the wire is bent into a circle of a given cross sectional area and resistance. When we are asked to find the resistance between two diametrically opposite points, we are basically finding the resistances of two semicircles. The resistance of each semicircle will be half of the resistance of the wire, that is $\dfrac{R}{2}$.

Now we need to find the connection, the wire looks like something like,

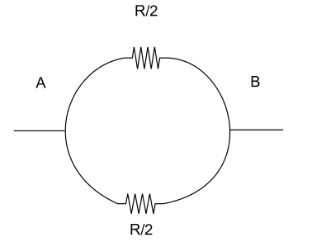
If we observe closely, we can see that the semicircles are in parallel connection, now we find the equivalent by using the formula,
${R_{eq}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$
We get,

\Rightarrow {R_{eq}} = \dfrac{{\dfrac{R}{2} \times \dfrac{R}{2}}}{{\dfrac{R}{2} + \dfrac{R}{2}}} \\\ \Rightarrow {R_{eq}} = \dfrac{{\dfrac{{{R^2}}}{4}}}{{\dfrac{{2R}}{2}}} \\\ \therefore {R_{eq}} = \dfrac{R}{4}$$ **Therefore, the correct answer is option A.** **Note:** The value of the resistance of the two semi circles can also be found using the cross-multiplication method. That is, we know the resistance for the whole circle, and we have to find it for half of the value $$2\pi r = R$$ We have to find the resistance for half of the circle, that is for $$\pi r$$. We divide both sides of the above equation with $$2$$ and get, $$\pi r = \dfrac{R}{2}$$ As you can see, this is the same value we got before. This is because the resistance of a wire is directly proportional to its length. $R \propto l$ Now, we also know that if two resistors are connected in parallel combination, then the equivalent resistance of the system is half of the resistance of the individual resistor. So, we get the final answer as $$\dfrac{R}{4}$$.