Question
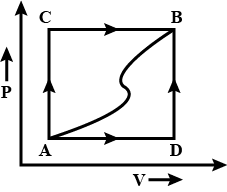
Question: When a system is taken from state A to state B along the path ACB, 80J of heat flows into the system...
When a system is taken from state A to state B along the path ACB, 80J of heat flows into the system and the system does 30J of work.
(a) How much heat flows into the system along the path ADB if the work done is -10J?
(b) When the system returns from state B to A along the curved path, the work done on the system is 20J. Does the system absorb or liberate heat, and how much?
(c) If UD−UA=40J, find the heat absorbed in the process AD and DB.
Solution
There is an inherent energy in every system which is known as internal energy of that system and this energy is due to the molecular state of motion of matter. Generally internal energy is represented by the symbol U.
Complete answer:
The main property of internal energy is it is independent of the path followed. So change in internal energy from A to B is calculated by adding work done and heat flows on system as follows:
ΔU(A→B)=q(ACB)+w(ACB)=80−30=50J
(a) How much heat flows into the system along the path ADB if the work done is -10J?
ΔU=50J=q(ADB)+w(ADB); q(ADB)=50−10=40J
(b) When the system returns from state B to A along the curved path, the work done on the system is 20J. Does the system absorb or liberate heat, and how much?
q(B→A)=ΔU(B→A)−w(B→A)=−50−20=−70J
Negative sign corresponds to the heat of 70J.
(c) If UD−UA=40J, find the heat absorbed in the process AD and DB.
ΔU(ADB)=ΔU(A→D)+ΔU(D→B);ΔU(D→B)=50−40=10J
Again,
ΔU(D→B)=q(D→B)+w(D→B)
We know that v(D→B)= 0, therefore w(D→B)= 0
So ΔU(D→B)=q(D→B)=10J
Now, q(ADB)=q(A→D)+q(D→B)
q(A→D)=40−10=30J
Note:
Internal energy is generally temperature dependent; it increases as we increase the temperature and also with the changes of states like from solid to liquid or from liquid to gas. Internal energy is a state function of a system and termed as an extensive quantity.
