Solveeit Logo
Login

Question

Question: When a ring is rolling \({V_1}\), \({V_2}\), \({V_3}\) and \({V_4}\) are velocities of top most poin...

When a ring is rolling V1{V_1}, V2{V_2}, V3{V_3} and V4{V_4} are velocities of top most point, lowest point, end point of horizontal diameter, centre of ring respectively, the decreasing order of these velocities is:
A. V2,V1,V4,V3{V_2},{V_1},{V_4},{V_3}
B. V2,V1,V3,V4{V_2},{V_1},{V_3},{V_4}
C. V1,V2,V3,V4{V_1},{V_2},{V_3},{V_4}
D. V1,V3,V4,V2{V_1},{V_3},{V_4},{V_2}

Explanation

Solution

Here we see that the ring is performing the rolling motion then the velocities at the different point on the ring will be different but the velocity of the centre of mass will be Vcm=rω{V_{cm}} = r\omega , where r=r = radius of the ring and ω=\omega = angular velocity of the centre of mass. So, with the help of the relation we can relate the velocities of the ring at its different points.

Complete answer:
Firstly we will draw a diagram depicting the velocities given as V1{V_1},V2{V_2},V3{V_3} and V4{V_4} are velocities of top most point, lowest point, end point of horizontal diameter, centre of ring respectively,

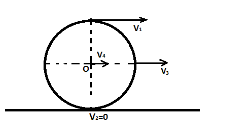
The velocity at the lowermost point is zero, since it will act like a stationary point.
So, V2=0{V_2} = 0----equation (1)
The velocity at the topmost point is,
V1=ωR+Vcm{V_1} = \omega R + {V_{cm}}
⇒V1=2Vcm\Rightarrow {V_1} = 2{V_{cm}}---equation (2)
The velocity at the end point of horizontal diameter,
V3=(Vcm)2+(Vcm)2=2(Vcm){V_3} = \sqrt {{{({V_{cm}})}^2} + {{({V_{cm}})}^2}} = \sqrt 2 ({V_{cm}})(this velocity will be having two component one is having magnitude ωR\omega Rdownwards and another in the direction of the velocity of the centre of mass)
So, V3=2(Vcm){V_3} = \sqrt 2 ({V_{cm}})-------equation (3)
Now thaw velocity of the centre of the ring,
V4=Vcm{V_4} = {V_{cm}}--------equation (4) (same velocity as that of the velocity of the centre of the mass)
Now on comparing the four equations we find that the velocity at the bottommost point is lowest while the velocity at the topmost most point is highest.
Hence the decreasing order of these velocities is as follows,
V1>V3>V4>V2{V_1} > {V_3} > {V_4} > {V_2}

So, the correct answer is “Option D”.

Note:
In a circular motion both linear and angular velocities are found. Angular velocity is a vector quantity having both direction and the magnitude. Angular velocity in a circular motion is the obtained by dividing the angular displacement by the time taken for the travel. To perform a circular motion there is a need of centripetal force which makes the circular motion possible. Centripetal force is the force that is necessary to keep an object moving in a curved path and that is directed inward toward the centre of rotation. There is another force in a circular motion that is known as centrifugal force. Centrifugal force is defined as the apparent force that is felt by an object moving in a curved path that acts outwardly away from the centre of the rotation.