Question

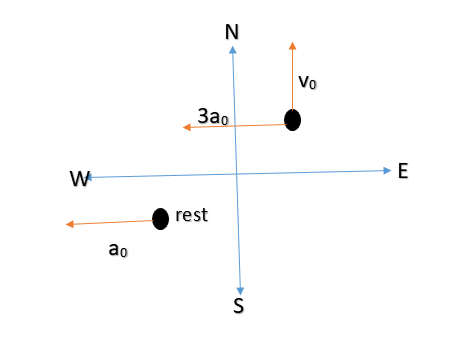
When a proton is released from rest in room, it starts with an initial acceleration ${{a}_{0}}$ towards west when it is projected towards north with a speed ${{v}_{0}}$ it moves with an initial acceleration $3{{a}_{0}}$ towards west. The electric and magnetic fields in the room are:
$\begin{aligned} & \text{A}\text{. }\dfrac{m{{a}_{0}}}{e}east,\dfrac{3m{{a}_{0}}}{e{{v}_{0}}}down \\\ & \text{B}\text{. }\dfrac{m{{a}_{0}}}{e}west,\dfrac{3m{{a}_{0}}}{e{{v}_{0}}}up \\\ & \text{C}\text{. }\dfrac{m{{a}_{0}}}{e}west,\dfrac{2m{{a}_{0}}}{e{{v}_{0}}}down \\\ & \text{D}\text{. }\dfrac{m{{a}_{0}}}{e}east,\dfrac{3m{{a}_{0}}}{e{{v}_{0}}}up \\\ \end{aligned}$

Answer 1

First when the object is at rest it will only experience electric force not magnetic force. Because the magnetic force on a charged particle at rest is zero. So when the proton is released from rest it will only experience electric force and will move. The direction of the electric force will be in the same direction as acceleration. Now calculate the electric force on the proton due to the electric field and equate it with the force due to Newton’s second law. You will get the electric field. Similarly when the proton is projected it will experience a magnetic force. Calculate the change in acceleration of the proton and calculate the force applying Newton’s second law. Equate this with magnetic force to get the magnetic field.

Formula used:
According to Newton’s second law ,the force on an object of mass $m$ and acceleration $a$ is given by $\overrightarrow{F}=m\overrightarrow{a}$ (in the direction of acceleration)
When a charged particle moves in a region having both electric field ($\overrightarrow{E}$) and magnetic field $\left( \overrightarrow{B} \right)$ it will experience both the electric force and magnetic force. And is given by
$\overrightarrow{F}=\overrightarrow{{{F}_{e}}}+\overrightarrow{{{F}_{m}}}=q\overrightarrow{E}+q\left( \overrightarrow{v}\times \overrightarrow{B} \right)$
Where, $v$ is the velocity of the charged particle.
Charge on a proton, $e=1.6\times {{10}^{-19}}C$

Complete answer:
Let the charge on the proton is ${{q}_{p}}=e$ and the mass of the proton be $m={{m}_{p}}$.
According to the question releasing the proton at rest it starts with initial acceleration ${{a}_{0}}$ in the west direction.

Now the force on the proton is only electric force and is given by
${{F}_{e}}={{q}_{p}}E=eE$
There will be no initial magnetic force because the proton initially rests.
Force on the proton when its mass is ${{m}_{p}}$ and acceleration ${{a}_{0}}$ is
$F={{m}_{p}}{{a}_{0}}$
This force will be equal to the electrostatic force.i.e

$\begin{aligned} & {{F}_{e}}=F \\\ & \Rightarrow eE={{m}_{p}}{{a}_{0}}\Rightarrow E=\dfrac{{{m}_{p}}{{a}_{0}}}{e} \\\ \end{aligned}$

The direction of the electric field will be in the direction of acceleration i.e. along west.
Magnetic force on the proton when the initial velocity ${{v}_{0}}$ is
${{F}_{m}}={{q}_{p}}\left( {{v}_{0}}\times B \right)=e{{v}_{0}}B$
The force on the object when the acceleration changes from ${{a}_{0}}$ to $3{{a}_{0}}$ is
$F'={{m}_{p}}(3{{a}_{0}}-{{a}_{0}})={{m}_{p}}2{{a}_{0}}$
This force is due to the magnetic field so

$\begin{aligned} & {{F}_{m}}={F}' \\\ & \Rightarrow e{{v}_{0}}B={{m}_{p}}2{{a}_{0}} \\\ & \Rightarrow B=\dfrac{{{m}_{p}}2{{a}_{0}}}{e{{v}_{0}}} \\\ \end{aligned}$
The direction of the magnetic field will be downward.

So, the correct answer is “Option C”.

Note:
When a charge moves in a region having both electric field and magnetic field it will be acted upon by two forces one is electric force and one is magnetic force. This force is called the Lorentz force. Note that there will be no magnetic force if the charge particle is at rest.