Question
Question: When a potential difference of \({10^3}\) volt is applied between A and B , a charge of \[0.75mC\] i...
When a potential difference of 103 volt is applied between A and B , a charge of 0.75mC is stored in the system of capacitor as shown . The value of C is (in μF ) is:
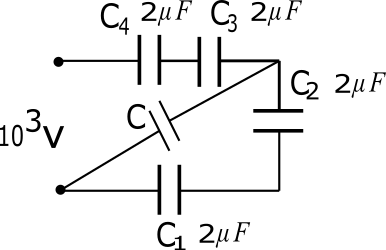
A) 21
B) 2
C) 2.5
D) 3
Solution
First we can calculate the equivalent capacitance of system of capacitors by using given information that the charge stored in system of capacitors is 0.75mC and voltage across the terminal is 103 volt. And we can calculate equivalent capacitance of circuit by using circuit diagram ,by using combination formula for series and parallel combination of capacitor
Complete step by step solution:
By the definition of capacitance we know charge stored in capacitor per unit potential difference is given by
⇒C=VQ
In question it is given the charge stored in a system of given capacitors or charge stored in equivalent capacitor Q=0.75mC or Q=0.75×10−3C.
V is given potential across the terminal is 103 volt
So the equivalent capacitance of the given circuit is Ceq=VQ
⇒Ceq=1030.75×10−3
Solving this
⇒Ceq=0.75×10−6F
⇒Ceq=0.75μF .................. (1)
So the equivalent capacitance of given system of capacitors is 0.75μF
Step 2
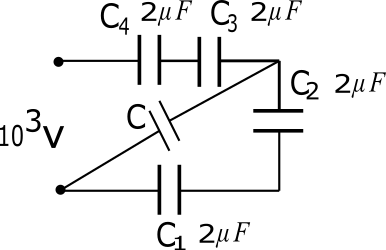
Now look at the circuit it is clear from circuit capacitor C1 and C2 are connected in series so series combination equivalent capacitance of C1 and C2 is C12 can calculate as
⇒C121=C11+C21
Put the value of C1 and C2
⇒C121=21+21
⇒C121=11
Hence C12=1μF
And C3 and C4 are also connected in series so equivalent capacitance C34 can be calculate as:
⇒C341=C31+C41
Put value of C3,C4
⇒C341=21+21
⇒C341=11
⇒C34=1μC
Hence we can replace C1,C2 by their resultant C12 and C3,C4 by their resultant C34 in circuit then circuit become.
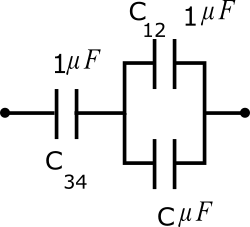
Now in this circuit C12 and C connected in parallel so the resultant capacitance can calculate by
⇒C12c=C12+C
⇒C12c=1+C
Now circuit become
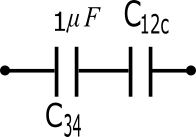
Now C34 and C12c is in series so
Equivalent capacitance of whole circuit
⇒Ceq1=C341+C12c1
Put values
⇒Ceq1=11+(1+C)1
Solving this
⇒Ceq1=(1+C)1+C+1
⇒Ceq1=(1+C)(2+C)
So the equivalent capacitance of given whole circuit is
⇒Ceq=(2+C)(1+C) ...................... (2)
Equation (1) and (2) both are representing the equivalent capacitance of given circuit
So (1) = (2)
⇒(2+C)(1+C)=0.75
⇒C+1=0.75(C+2)
⇒C+1=0.75(C)+1.50
Again solving this
⇒C−0.75(C)=1.50−1
⇒C(1−0.75)=0.50
Further solving
⇒C=0.250.50
∴C=2μF
Hence in given circuit the value of C is 2μF.
So option B is correct.
Note: We use here series combination formula for calculating equivalent capacitance let’s talk about this. If capacitors connected in series then the charge stored in every capacitor same but the voltage across every capacitor different let take three capacitor connected in series voltage across capacitors C1,C2 and C3 is V1,V2 and V3 respectively
V1=C1q,V2=C2q,V3=C3q
Net voltage V=V1+V2+V3
⇒V=C1q+C2q+C3q
If equivalent capacitance is Ceq then V=Ceqq
⇒Ceqq=C1q+C2q+C3q
So we get
∴Ceq1=C11+C21+C31.
