Question

When a polar bear jumps on an iceberg, its weight 200kg-wt is just sufficient to sink the iceberg. What is the weight of the iceberg? (specific gravity of ice is 0.9 and that of sea water is 1.02).
A. 1500 kg-wt
B. 180 kg-wt
C. 1800 kg-wt
D. 320 kg-wt

Answer 1

The net downward force on the iceberg will be balanced by the buoyant force exerted by the sea water on the iceberg, in the upward direction. The net downward force on the iceberg will be the sum of the weights of the bear and the iceberg. Then by using the formula for the buoyant force find the upward force. Equate the two forces to find the weight of the iceberg.

Formula used:
${{F}_{g}}=W$
W=mg
${{F}_{B}}={{\rho }_{l}}g{{V}_{s}}$
$volume=\dfrac{density}{mass}$
$\rho =s\times {{10}^{3}}kg{{m}^{3}}$

Complete step by step answer:
It is given that when the polar bear jumps on the iceberg, the iceberg just sinks in the sea water. This means that the net gravitational force on the iceberg acting downwards is equal to the buoyant force exerted by the sea water in the upward direction.
i.e. ${{F}_{g}}={{F}_{B}}$.

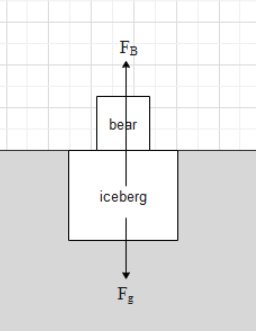
Here, the net gravitational force on the iceberg will be the sum of the gravitational force on the bear and the gravitational force on the iceberg. The gravitational force on the bear will be equal to the weight of the bear, i.e. 200 kg-wt. Let the weight of the iceberg be W.
Then,
$\Rightarrow {{F}_{g}}=W+200$ ….. (i)
The buoyant force on the iceberg will be equal to ${{F}_{B}}={{\rho }_{l}}g{{V}_{s}}$ ….. (ii).
Here, ${{\rho }_{l}}$is the density of the liquid (sea water), g is acceleration due to gravity and ${{V}_{s}}$ is the submerged volume of the iceberg (in this case, it is the whole volume of the iceberg).
Density of a body is given as $\rho =s\times {{10}^{3}}kg{{m}^{3}}$, where s is the specific gravity of the body.
Therefore,
${{\rho }_{l}}=1.02\times {{10}^{3}}kg{{m}^{3}}=1020kg{{m}^{3}}$.
Let us calculate ${{V}_{s}}$.
We know that $volume=\dfrac{density}{mass}$.
Let the mass of the iceberg be m.
The density of the iceberg is ${{\rho }_{i}}=0.9\times {{10}^{3}}kg{{m}^{3}}=900kg{{m}^{3}}$.
Hence, ${{V}_{s}}=\dfrac{m}{{{\rho }_{i}}}=\dfrac{m}{900}$.
Substitute the values of ${{V}_{s}}$ and ${{\rho }_{l}}$ in equation (ii).
$\Rightarrow {{F}_{B}}=1020g\left( \dfrac{m}{900} \right)=\dfrac{1020}{900}mg$.
We know that the weight of the iceberg is equal to W=mg, (i.e. the gravitational force on the iceberg).
$\Rightarrow {{F}_{B}}=\dfrac{1020}{900}W$.
Since ${{F}_{g}}={{F}_{B}}$,
$W+200=\dfrac{1020}{900}W$
$\Rightarrow 900W+900\times 200=1020W$
$\Rightarrow W=\dfrac{900\times 200}{120}=1500kg-wt$

Hence, the correct option is A.

Note:
Note that the unit kg-wt in the given question is a unit of force and not a unit of mass.
The value of 1 kg-wt is equal to 1 N.
The buoyant force is also stated as the weight of the liquid that is displaced by an object that is submerged in it. Therefore, we can also find the weight of the volume of liquid displaced to find the buoyant force.