Question

When a person throws a meter stick it is found that the centre of the stick is moving with the speed of 10 m/s vertically upwards and the left end of the stick with a speed of 20 m/s vertically upwards. Then the angular speed of the stick is:
A. 20 rad/sec
B. 10 rad/sec
C. 30 rad/sec
D. None of the above.

Answer 1

In this question we have been asked to calculate the angular velocity of the meter stick. It is given that the centre of stick is moving vertically upward with velocity of 10 m/s and the left end with velocity of 20 m/s. Therefore, to solve this question we shall use the concept of relative velocity. We shall calculate the velocity with respect to centre and then calculate the angular velocity using the result.
Formula Used:
$V=r\omega$
V is the velocity of stick
$\omega$ is the angular velocity
r is the distance

Complete answer:
It is given that a person throws a stick upwards. Let the velocity of the stick be as shown in the figure below.

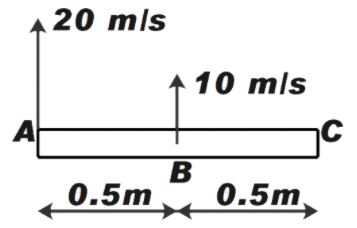
Now, let velocity of left point A be ${{V}_{A}}$ and the center point be ${{V}_{B}}$.
Now, assuming the point B is brought to rest i.e. the velocity of point A with respect to point B is
${{V}_{AB}}=20-10$
Therefore,
${{V}_{AB}}=10m/s$
Now, we know that,
$V=r\omega$
It is given that the length of stick is 1 metre. Therefore, length of centre from the left point is 0.5 m
Therefore,
${{V}_{AB}}=0.5\omega$
Therefore,
$\omega =\dfrac{10}{0.5}$
On solving
We get,
$\omega =20rad/\sec$

Therefore, the correct answer is option B.

Note:
The angular velocity of the object is the parameter that determines how fast an object will rotate with relative to a point. It is also defined as the rate of change of angle of an object with respect to a certain point. There are two types of angular velocity, spin angular velocity and orbital angular velocity.