Question

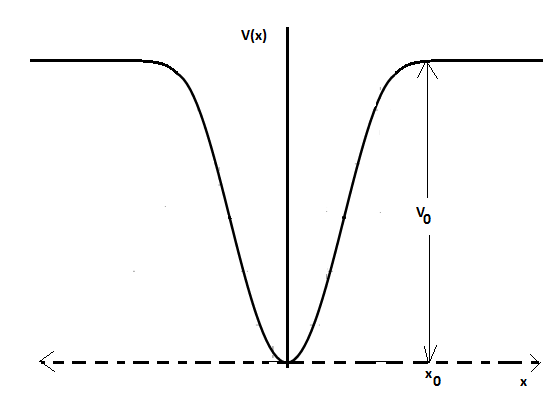
When a particle of mass $m$ moves on the x-axis in a potential of the form $V\left( x \right)=k{{x}^{2}}$, it performs simple harmonic motion. The corresponding time period is proportional to $\sqrt{\dfrac{m}{k}}$, as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of $x=0$ in a way different from $k{{x}^{2}}$ and its total energy is such that the particle does not escape to infinity. Consider a particle of mass $m$ moving on the x-axis. Its potential energy is $V\left( x \right)=\alpha {{x}^{4}}$ $\left( \alpha >0 \right)$for $\left| x \right|$near the origin and becomes a constant equal to ${{V}_{0}}$ for $\left| x \right|\ge {{x}_{0}}$ (see figure).
For periodic motion of small amplitude $A$, the time period $T$ of this particle is proportional to:

$A)A\sqrt{\dfrac{m}{\alpha }}$
$B)\dfrac{1}{A}\sqrt{\dfrac{m}{\alpha }}$
$C)A\sqrt{\dfrac{\alpha }{m}}$
$D)A\sqrt{\dfrac{2\alpha }{m}}$

Answer 1

Using dimensional analysis we can solve this question. Here, we have the same three variables in all four options, i.e., $\text{A, }\\!\\!\alpha\\!\\!\text{ and m}$. Find the dimension of each variable, and check options one by one to see which one has the same dimension as time period.
Formula used:
$P.E=mgh$

Complete step by step answer:

Using dimensional analysis, we can solve this question.
Dimension of time period, $\left[ T \right]=\left[ {{M}^{0}}{{L}^{0}}{{T}^{1}} \right]$
Now,
Let’s find out the dimension of $\text{ }\\!\\!\alpha\\!\\!\text{ }$.
Given that,
$V\left( x \right)=\alpha {{x}^{4}}$,$\left( \alpha >0 \right)$ ---- 1
From equation 1, we get,
$\alpha =\dfrac{V\left( x \right)}{{{x}^{4}}}$
Here$V\left( x \right)$is potential energy and $x$indicates length.
Let’s find the dimensions of potential energy and length.
Potential energy, $P.E=mgh$ -------1
Where,
$m$ is the mass of the object
$g$ is the acceleration due to gravity
$h$ is the height
We have,
$\left[ m \right]=\left[ {{M}^{1}} \right]$
$\left[ g \right]=\left[ {{M}^{0}}{{L}^{1}}{{T}^{2}} \right]$
$\left[ h \right]=\left[ {{L}^{1}} \right]$
Substitute dimensions of $\text{m,g and h}$ in equation 1. We get,
$\left[ P.E \right]=\left[ {{M}^{1}} \right]\times \left[ {{M}^{0}}{{L}^{1}}{{T}^{2}} \right]\times \left[ {{L}^{1}} \right]=\left[ {{M}^{1}}{{L}^{2}}{{T}^{-2}} \right]$
Dimension of length, ${{\left[ x \right]}^{4}}={{\left[ {{M}^{0}}{{L}^{1}}{{T}^{0}} \right]}^{4}}=\left[ {{M}^{0}}{{L}^{4}}{{T}^{0}} \right]$
Then,
$\dfrac{V\left( x \right)}{{{x}^{4}}}=\dfrac{\left[ {{M}^{1}}{{L}^{2}}{{T}^{-2}} \right]}{\left[ {{M}^{0}}{{L}^{4}}{{T}^{0}} \right]}=\left[ {{M}^{1}}{{L}^{-2}}{{T}^{-2}} \right]$
$\left[ \alpha \right]=\left[ {{M}^{1}}{{L}^{-2}}{{T}^{-2}} \right]$
Here, $A$is amplitude. Then, $\left[ A \right]=\left[ {{L}^{1}} \right]$
We have, $\left[ m \right]=\left[ {{M}^{1}} \right]$
Then, checking options we can see that the dimension of the equation in the third option has the same dimension as the time period.
$\left[ \dfrac{1}{A}\sqrt{\dfrac{m}{\alpha }} \right]=\dfrac{1}{\left[ {{L}^{1}} \right]}\times \dfrac{{{\left( \left[ {{M}^{1}} \right] \right)}^{\dfrac{1}{2}}}}{{{\left( \left[ {{M}^{1}}{{L}^{-2}}{{T}^{-2}} \right] \right)}^{\dfrac{1}{2}}}}=\dfrac{\left[ {{M}^{\dfrac{1}{2}}}{{L}^{0}}{{T}^{0}} \right]}{\left[ {{M}^{\dfrac{1}{2}}}{{L}^{0}}{{T}^{-1}} \right]}=\left[ {{M}^{0}}{{L}^{0}}{{T}^{1}} \right]$
$\left[ T \right]=\left[ \dfrac{1}{A}\sqrt{\dfrac{m}{\alpha }} \right]=\left[ {{M}^{0}}{{L}^{0}}{{T}^{1}} \right]$

So, the correct answer is “Option B”.

Note:
Dimensional analysis has many applications. It can be used to convert a physical quantity from one system to another. Also dimensional analysis can be used to check the correctness of a physical relation and to obtain relationships among various physical quantities involved.