Question

When a parallel beam of light in air is incident on the surface of a transparent medium the reflected beam is found to be completely plane polarized. The refracted beam in the medium suffers a deviation of ${20^ \circ }$ from its original path in air. Calculate the refractive index of the material of medium.

Answer 1

When the incident light after reflection becomes completely plane polarized after striking a transparent medium, the angle of incidence formed is called the Brewster’s angle. Brewster's law is applied in-order to find the angle of refraction and then the refractive index of the medium.

Complete answer:
The above problem revolves around the concept of polarization by reflection given by Brewster’s law. In the question, it is given that the ray reflected from the surface is completely plane polarized which means that its vibrations become perpendicular to the plane of incidence. Before looking into the law we need to know the concept behind Brewster’s angle.

When light is incident on a transparent medium its property is to reflect and this reflected ray is said to be partially polarized. At a particular condition, at a certain angle of incidence the reflected light is completely plane polarized. The angle of incidence at which a beam of unpolarized light falling on a transparent surface is reflected as a beam of completely plane polarized light is called the polarizing or the Brewster’s angle. This angle is denoted by ${i_p}$. A special condition when this happens is that the sum of the polarizing angle and the angle of refraction is equivalent to ${90^ \circ }$. The reflected ray of light is at right angles with the refracted ray. The equation obtained is hence as follows:
${i_p} + {r_p} = 90$ ------($1$)
Where, ${i_p}$ is the Brewster’s angle or the polarizing angle and ${r_p}$ is the angle of refraction.

It is given that the angle of deviation is ${20^ \circ }$. This is given to be the angle which the refracted beam suffers from the path it is originally supposed to travel in. By the definition of the angle of deviation we know that it is the angle between the extended incident ray and the refracted ray is the angle deviated. The figure given below illustrates the same.

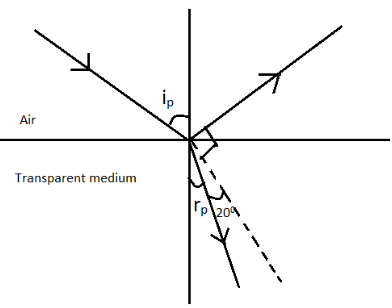
The path of the light inside the medium is originally supposed to travel through the path given by the dotted lines but it gets refracted and forms an angle, ${r_p}$ with the normal as per Brewster's law. Hence we can conclude that the sum of the angle of deviation suffered and the angle of refraction is equivalent to the angle of incidence by the alternative angle property because the dotted line given in the diagram is just the extension of the incident ray inside the medium. Hence we can construct the following equation:
${i_p} = {r_p} + 20$------($2$)

The value of angle of incidence is determined in terms of angle of refraction. After substituting the equation ($2$) in ($1$) we get:
${r_p} + 20 + {r_p} = 90$
By solving out the above equation we get the value of angle of refraction:
$2{r_p} + 20 = 90$
$\Rightarrow 2{r_p} = 90 - 20$
$\Rightarrow 2{r_p} = 70$
$\Rightarrow {r_p} = {35^ \circ }$
Next, we apply the Brewster’s law equation. It states that the tangent of the polarizing or the Brewster’s angle is equivalent to its refractive index. Hence it is given by the following equation:
$\mu = \tan {i_p}$ -----($3$)
Where, $\mu$ is the refractive index of the transparent medium.

The value of angle of refraction obtained is substituted in ($1$) to get the value of the polarization angle. By rearranging the terms from ($1$) we know that:
${i_p} = 90 - {r_p}$
$\Rightarrow {i_p} = 90 - 35$
$\Rightarrow {i_p} = {55^ \circ }$
Now that we have found out the value of Brewster’s angle we substitute this value in equation ($3$). We get:
$\mu = \tan \left( {55} \right)$
$\therefore \mu = 1.428$

Hence the refractive index of the medium is $1.428$.

Additional information: Un-polarized light is one that has both types of vibrations one being perpendicular and one being parallel to the plane of incidence. The equation for Brewster’s angle is obtained from Snell's law of reflection and this value of Brewster’s angle depends on the nature of the transparent medium and the wavelength of the incident light.The French physicist Malus discovered the partial plane polarization of the reflected ray when light is incident on a transparent medium in $1808$. The British physicist David Brewster was responsible for the discovery of the condition that the reflected and the refracted rays are perpendicular to each other and hence the law was named after him.

Note: The angle of refraction could be mistaken and taken to be as the angle deviated which seems to be a common error. The formation of the Brewster’s angle is said to be a special condition where the medium considered here is strictly a transparent medium and the law is only applicable when the reflected ray is at right angles to the refracted ray.