Question
Question: When a mass \(m\) which is vibrating with spring of spring constant \({{k}_{1}}\). Its frequency wi...
When a mass m which is vibrating with spring of spring constant k1. Its frequency will be 3Hz and with spring of spring constant k2 and its frequency will be 6Hz. Then what will be the frequency of oscillations when mass is connected with spring as represented in the diagram?
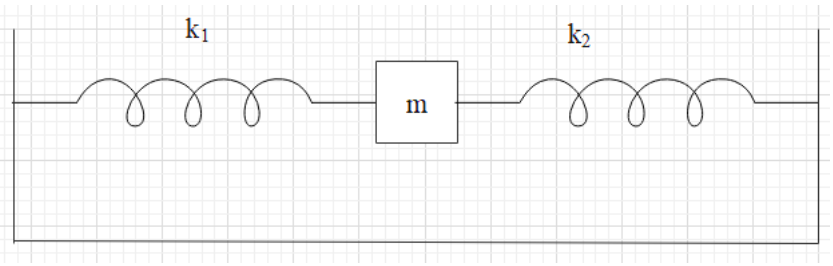
Solution
The frequency can be found by taking the square root of the ratio of the spring constant to the mass of the spring. Find out the equation for both the spring constant. As these two springs are parallel then their resultant spring constant will be found by taking the sum of both the spring constant. Calculate the resultant frequency also. This will help you in answering this question.
Complete answer:
The frequency can be found by taking the square root of the ratio of the spring constant to the mass of the spring. That is,
ω1=mk1
As the frequency has been mentioned to be 3Hz, substituting this in the equation will give,
