Question

When a load of$10\,kg$ is suspended on a metallic wire, its length increases by $2\,mm.$The force constant of the wire is

Answer 1

Load is given which is $10\,kg$and when it is applied the length increases by$2\,mm.$So, here the concept of Hooke’s Law applies $(F = - Kx)$ .

Complete step by step answer:
According to question, here are two forces apply on wire which holds the wire equilibrium; the forces are:
(i) Restoring force$(F = - Kx)$
(ii) Weight$(mg)$
$m$ is the mass of load$= 10\,kg$
$K$ is force constant of wire
$x$ is expansion on wire
$g$ is gravity acceleration
Now according to Hooke's law, Restoring force is proportional to the extension in wire
So, $F = Kx$
Also the force applied that causes extension is the weight
So, 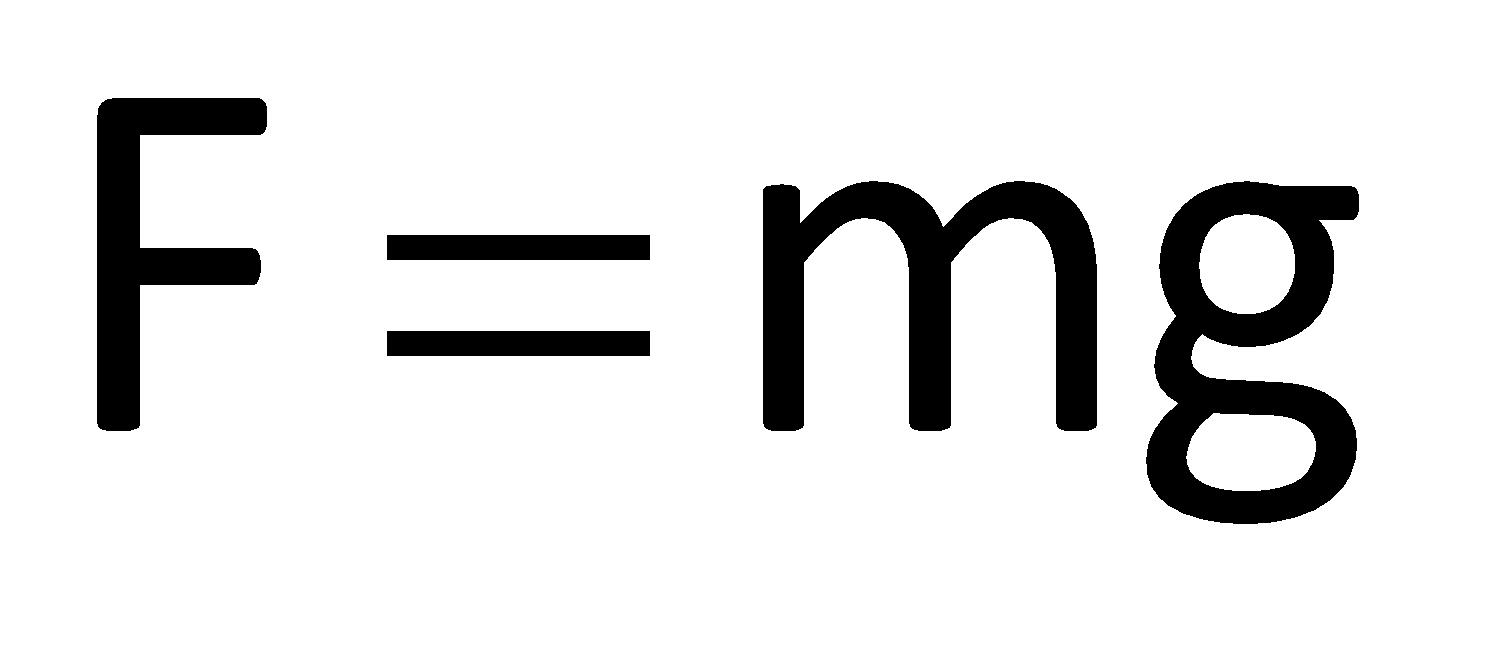(weight of load)
Here, wire is in equilibrium that means both the forces will be equal that is:
$Kx = mg$
K = \dfrac{{mg}}{x} \\\
K = \dfrac{{10 \times 10}}{{2 \times {{10}^{ - 3}}}} \\\
\left[ {K = 5 \times {{10}^4}\,N/m} \right] \\\
So, the force constant of wire $5 \times {10^4}\,N/m$

Additional Information:
To solve the question we should remember that:
(i) If increase or decrease of wire is given and we have to calculate force constant then use Hooker’s Law.
(ii) Wire is in equilibrium, so net force$= 0$.

Note:
All the quantities need to be in the same units. As the value of x is in mm while all others are in SI units so in order to get the correct answer x need to be converted into meters.Also remember there are two forces in the given diagram.