Question

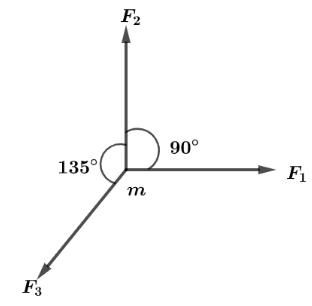
When a force $F$ acts on a body of mass $m$, the acceleration produced in the body is a. If three equal forces ${F_1},{F_2}$ and ${F_3}$ which are related as ${F_1} = {F_2} = {F_3} = F$ act on the body as shown in the figure. Then the acceleration produced is:

A. ( $\sqrt 2 - 1$ ) $a$
B. ( $\sqrt 2 + 1$ ) $a$
C. ( $\sqrt 2$ ) $a$
D. $a$

Answer 1

Whenever a body is acted by some force it gets accelerated which in mathematical form it’s called Newton’s second law of motion as $F = ma$ here, we will find the net force acting on the body and its direction then will find the net acceleration of the body.

Complete step by step answer:
Let us find the net magnitude of forces ${F_1}$ and ${F_2}$ which are perpendicular to each other and this net force be written as ${F_{12}}$ so,
${F_{12}} = \sqrt {{F^2} + {F^2}}$
${F_{12}} = \sqrt 2 F$ Which will be in direction just opposite to that of ${F_3}$ .
Now, two forces acting on the body of mass m respectively ${F_{12}} = \sqrt 2 F$ and ${F_3} = F$.
Both forces are in opposite direction,
Hence net force act on the body of mass $m$ is,
${F_{net}} = \sqrt 2 F - F$
$\Rightarrow {F_{net}} = (\sqrt 2 - 1)F$
Now, let us assume that net acceleration is denoted by $a'$ then by newton’ second law we have:
$(\sqrt 2 - 1)F = ma'$
We also know that, $F = ma$ put this value in above equation, we get,
$(\sqrt 2 - 1)a = a'$
Net acceleration is $a' = (\sqrt 2 - 1)a$

Hence, the correct option is A.

Note: It should be remembered that, Force is a vector quantity and its added always using vector algebra which is given as ${F_{net}} = \sqrt {{F_1}^2 + {F_2}^2 + 2{F_1}{F_2}\cos \theta }$ and the direction of two equal vectors resultant is in the middle of the angle between them. And it can also be calculated with the general formula $\tan \beta = \dfrac{{{F_2}\sin \theta }}{{{F_1} + {F_2}\cos \theta }}$.