Question

When a capacitor of value 200 $\mu F$ charged to $200V$ is discharged separately through resistance of $2\Omega$ and $8 \Omega$, then heat produced in joule will respectively be:

Answer 1

In order to solve the question, we will first apply the formula of potential energy in the stored capacitor then we will deduce the heat energy that is dissipated in the process of discharge and hence we will get the total heat energy by adding all energy that in this case will be potential energy

Formula used:
$U = \dfrac{1}{2}C{V^2}$
Here, $U$ is the potential energy
$C$ is the capacitance
$V$ is the voltage

Complete step by step answer:
In the question we are given a capacitor which is first charged then it is discharged separately through resistances and the heat is produced and we have to find that heat produced
value of capacitor = 200 $\mu F$
potential difference till it is charged to = 200V
resistance = 2 ohms and 8 ohms


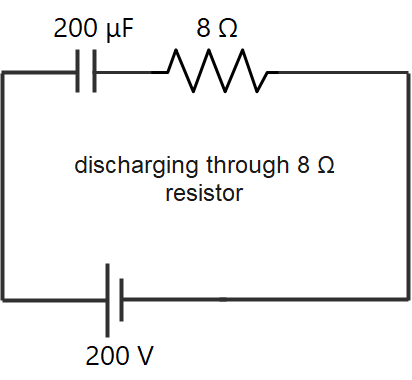
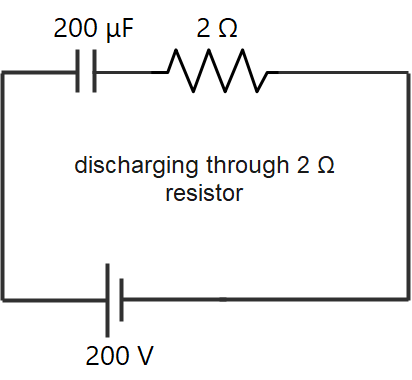
First, we will find the potential energy stored in the capacitor for that we will use the formula
$U = \dfrac{1}{2}C{V^2}$
Now we will substitute C = 200$\mu F$, V = 200 V
Changing capacitance from $\mu F$to F
1$\mu F$ = ${10^{ - 6}}F$
200$\mu F$ = 200 $\times$ ${10^{ - 6}}F$
After changing the $\mu F$ to F we will substitute the values
$U = \dfrac{1}{2} \times (200 \times {10^{ - 6}}F) \times {(200V)^2}$
Solving for potential energy we get
U = 4 Joules
On discharging all the energy that is in this case is potential energy in the capacitor will be dissipated as the heat through the connected resistor
Hence, Heat produced = 4 Joules
Here heat produced is independent of value of resistance connected so, in both the cases heat produced will be 4 Joules.

Note:
There might be a chance of confusing at how will the value of resistance will affect only in the time of discharging and not the heat as a time constant during the discharging the higher the value of resistance is the capacitor will take more time to discharge and hence the heat remains same in both cases