Question

When 6 identical cells of no internal resistance are connected in series in the secondary circuit of a potentiometer, the balancing length is $l$ . If two of them are wrongly connected the balancing length becomes.
A. $\dfrac{L}{4}$
B. $\dfrac{L}{3}$
C. $L$
D. $\dfrac{{2L}}{3}$

Answer 1

To answer the question, write the total emf of identical cells connected in series, and the balancing length is $l$ . After that, we will determine the emf of the two cells that are connected in the opposite direction with regard to the four other cells, and then we will find ${l_2}$ by the ratio of two emf of a battery is equal to the ratio of lengths. As a result, we'll apply this approach to figure out the unknown length.

Complete answer:
In order to answer the question, we will start solving it by writing the given values.
It is given to us in the question that $6$ identical cells are connected in series combination, and when the cells are connected in series, the battery's emf is equal to the total of the individual cells' emf.

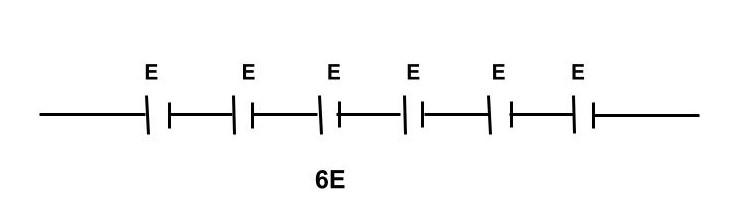
Therefore, total emf of the cell;
$E = 6E$
$\Rightarrow {E_1} = 6E$
And balancing length is $l$
Therefore, ${l_1} = l$
Now, it is said that two cells are connected wrongly, i.e. connected in opposite direction

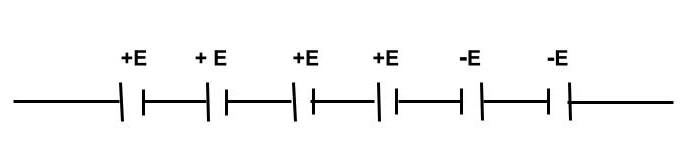
Therefore the emf $= E$ of wrongly connected cell will be $- E$
$\therefore$ Here total emf of these two will be
$E = 2E \\\ \Rightarrow {E_2} = 2E \\\$
So, we have to find balancing length after wrongly connection, i.e. ${l_2} = ?$
And in potentiometer,
Emf is directly proportional to Resistance and also directly proportional to the length i.e.
$Emf\left( E \right)\propto \,Resistance\left( R \right)\propto Length\left( l \right)$
Therefore,
$\therefore E\,\alpha \,\,l$
$\Rightarrow \dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{{l_1}}}{{{l_2}}}\,\,\,.........\left( {Formula} \right)$
Now, we will put all the values in the equation
$\Rightarrow \dfrac{{6E}}{{2E}} = \dfrac{l}{{{l_2}}}$
From here we will find out the required length ${l_2}$
$\therefore {l_2} = \dfrac{l}{3}$
Hence the balancing length after they are wrongly connected is $\dfrac{L}{3}$
The correct option is: (B) $\dfrac{L}{3}$.

Note:
The potentiometer, it should be noted, uses the comparative approach, which is more accurate than the deflection method. As a result, it's primarily used in situations where greater precision is necessary or no current flows from the source under examination. The potentiometer is a component of an electrical circuit that is used to control volume.